Как изменится площадь ромба если одна из его диагоналей увеличить в 4 раза а другую уменьшить в 5 раз

Площадь ромба =    .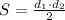

Если d₁ увеличить в 4 раза, то она станет равна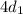    , а если d₂ уменьшить в 5 раз , то она станет равна  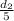  . Тогда площадь ромба будет равна  .

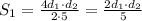Площадь нового ромба будет составлять 4/5 от площади заданного ромба, то есть площадь нового ромба меньше площади заданного ромба на (1/5)S .

Пусть d₁, d₂ - диагонали ромба, S - площадь ромба

Тогда S = 1/2d₁d₂

При изменении диагоналей ромба имеем

S₁ = 1/2(4d₁)(d₂/5) = 4/5*(1/2d₁d₂) = 4/5*S

Таким образом при изменении диагоналей площадь ромба уменьшится на 1/5 и будет равна 4/5 первоначальной площади.