Извлеките квадратный корень, если m<0, n<0 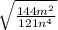
решите , с пояснениями

Другие вопросы по теме Алгебра
Популярные вопросы
- Определите степень окисления элементов в метане СН4 и карбиде алюминия Аl4С3. Какие...
3 - Напишите электронную формулу атома углерода в его возбужденном состоянии с квантовых...
3 - Оба элемента относятся к микроэлементам 1) железо и азот 2) молибден и цинк 3) бор...
3 - Брусок массы m1= 5 кг лежит на гладкой поверхности. На бруске лежит тело массой...
2 - Напишите электронную формулу атома кремния с квантовых ячеек в его основном и возбужденном...
2 - Определите простейшую формулу: а) соединения кальция с углеродом, содержащего 37,5%...
3 - Число электронных уровней и число электронов на внешнем уровне атома кремния равны...
3 - Три важнейших элемента минеральных удобрений 1) азот, фосфор и кальций 2) азот,...
2 - Определите элемент, атом которого имеет: а) три электронных уровня и четыре электрона...
2 - В партии из 15 деталей 10 стандартных. Найти вероятность того, что среди пяти взятых...
2
Воспользуемся формулой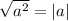 :
:
Модули и
и  раскрывали со сменой знака, так как m и n - отрицательные числа.
раскрывали со сменой знака, так как m и n - отрицательные числа.