Извлеките корень из выражения, если это возможно
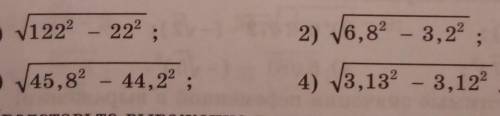
Другие вопросы по теме Алгебра
Популярные вопросы
- Какое из уравнений является квадратным а)2х-3х^2-12+x=0 b)-3x^2+2x+12=0 c)-3x^2-x+14=0...
1 - Разбор слова по составу слова вареник.однкоренные слова к словувареник...
2 - Сочинение на тему как быть здоровым для 4 класса...
3 - Закончить реакцию ионного обмена и написать ее в ионно-молекулярной форме hcoona+hno2...
2 - Определите массу углекислого газа, если его объем составляет 224л...
3 - Выполни деление с остатком в столбик показав первое промежуточное деление с знаков...
2 - Выберите правильное утверждение: а) гуманность-совокупность принципов и норм поведения...
1 - Реши вичисли запиши ответ в двух рулонах была 864 м плёнки сколько плёнки было в...
3 - Мəтіннен қазіргі кезде қайта жаңғырған атауларды тепіп жазыңдар...
2 - Попробуй объяснить своему иностранному сверстнику, изучающий язык, с какими падежами...
2
Объяснение:
Объяснение:
V- корень, делаем по формуле: a^2-b^2=(a-b)(a+b)
1) V((122-22)*(122+22))=V(100*144)=10*12=120
2) V((6,8-3,2)(6,8+3,2))=V(3,6*10)=V36=6
3) V((45,8-44,2)(45,8+4,2))=V(1,6*90)=V(16*9)=4*3=12
4) V((3,13-3,12)(3,13+3,12))=V(0,01*6,25)=0,1*2,5=0,25
по формуле: a^2-b^2=(a-b)(a+b)