1. Алгебра
  2. Известно, что Вычислите:

Известно, что
Вычислите: а)
б)
в)

​


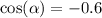
\cos( \alpha ) = - 0.6
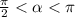
\frac{\pi}{2} < \alpha < \pi
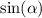
\sin( \alpha )
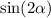
\sin(2 \alpha )
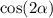
\cos(2 \alpha )

хотам3 хотам3    1   12.04.2021 05:21    0

Ответы
vaflya2007 vaflya2007  12.05.2021 05:32

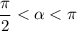Так \dfrac{\pi}{2} < \alpha < \pi, то рассматриваемый угол второй четверти, где синус положительный.

Используя основное тригонометрическое тождество, получим:

\sin^2\alpha +\cos^2\alpha =1

\sin^2\alpha =1-\cos^2\alpha

\sin\alpha =\sqrt{1-\cos^2\alpha}

\sin\alpha =\sqrt{1-(-0.6)^2}=0.8

Используя формулу синуса двойного угла, получим:

\sin2\alpha =2\sin\alpha \cos\alpha

\sin2\alpha =2\cdot0.8\cdot(-0.6)=-0.96

Используя формулу косинуса двойного угла, получим:

\cos2\alpha =\cos^2\alpha-\sin^2\alpha

\cos2\alpha =(-0.6)^2-0.8^2=-0.28

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Алгебра
rkarina79 rkarina79  19.07.2019 11:10
Lim x (стремится к бесконечности) 3x^3- 6 x+5/8-9x^3...
babayka76 babayka76  19.07.2019 11:10
Sin альфа cos2 альфа-sin(-альфа)sin2 альфа...
Анёк11 Анёк11  19.07.2019 11:10
При каких значениях параметра z уравнение cos^4x+6cos^2x-z=-5 не имеет решений?...
nmedvedeva20018 nmedvedeva20018  19.07.2019 11:10
2cos²a-2sin²a=1 a-альфа) решить, желатено пошагово)...
NastiaZaic NastiaZaic  19.07.2019 11:10
Чему равен |а| ,если 1)а больше 0 ; 2)а=0 ; 3)а меньше 0...
DashaK24 DashaK24  19.07.2019 11:10
Решите систему неравенств: 6(5х+1)-5(6х+1) х (х-3)(х+5) 0 решить,....
SosaLegor312lok SosaLegor312lok  19.07.2019 11:10
1)1=10x-25 x^2 2)в х^2+20=9в 3)17а=12+6а x^2 4)5х=х^2 5)-х^2+8=0 6)-24x=9+16x^2 7)2+3x^2=4x 8)x^2-11x=42 9)12x-35=x^2 10)14x-x^2=48...
yuliyamusatova1 yuliyamusatova1  19.07.2019 11:10
Диагональ прямоугольника равно 10см,а его периметр равен 28см.найдите сторлны прямоугольника...
bryuho20011 bryuho20011  19.07.2019 11:10
Теплоход за 2 часа км по озеру и 12 км по течению речки.найти скорость теплохода во время движения по озеру,если скорость течения речки равняется 4 км/ч....
GRISHINANASTYA GRISHINANASTYA  19.07.2019 11:10
Дано: a,b,x -натуральные числа, где x четное и a+b=x. найти число a, если значение a*b наибольшее. ответ - х/2. подскажите, , каким образом решать...

Популярные вопросы