Известно, что уравнение ax^2-(4a+4)x+3a+13=0 имеет действительные корни (1 или 2). при каких значениях параметра а каждый из корней меньше 1.
Ответы
Чтобы кв. ур. имело действ. корни, надо, чтобы дискриминант был >=0.
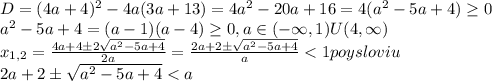
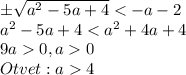
ПОКАЗАТЬ ОТВЕТЫ
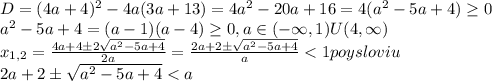
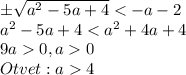
Другие вопросы по теме Алгебра
Популярные вопросы
- Скласти хронологічну таблицю відкриття органічних речовин (синтезу)...
3 - -2.5x+y=3.5 15-6y=-21 Решите сестему...
2 - Квантовые числа и определения...
1 - Шылауларды қатыстырып , ауа райының күрт өзгеруі себептеріне...
1 - это русский рт Ларионовой...
3 - Опишите конкретный случай РПД...
2 - Cross out the repeated words in each sentence. Write one or...
3 - Алгебра казакская школа 8 класс...
3 - Взгляды западников и славянофилов! Кратко...
1 - Учебное задание №1 Решите неравенства и изобразите множество...
3