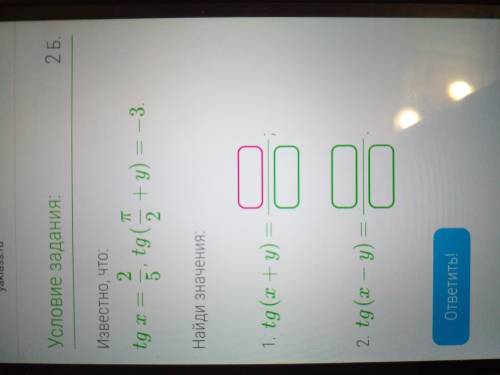
Известно, что: tg x = 2/5 , tg (pi/2+y) = -3
Найди значения:
1. tg (x+y)= ?/?
2. tg (x-y)= ?/?
Другие вопросы по теме Алгебра
Популярные вопросы
- Написать в тетради реакции взаимодействия ядра азота альфа частицами...
3 - ответьте на во понятие Понятия: перо, птицы,теплокровность,клюв,цевка,дыхательная...
1 - Кого Столыпин называет главной силой страны?...
2 - По рисунку 41 определите дисперсию в ангстремах на 1 мм длины спектра...
3 - Укажи варианты ответов, в которых во всех словах одного ряда пропущена...
3 - Задание 5.найти все значения параметра а, при которых неравенство...
3 - Балалар суға түсіп жүрген бассейннің ұзындығы 15м ені 8м,ал биіктігі...
2 - 2. Первый час автомобиль ехалсо скоростью 100 км/ч.а потом два...
1 - Как называется совокупность растительных популяций? фитоценоз биоценоз...
2 - Укажите имена существительные, в которых пишется окончание И: А)...
1
Формулы тангенса суммы и разности:
Известно, что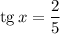 .
.
Также известно, что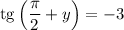
Воспользовавшись формулой приведения, запишем:
И так как тангенс и котангенс - взаимно обратные величины, получим:
Находим требуемые значения: