1. Алгебра
  2. Известно, что сумма квадратов

Известно, что сумма квадратов последовательный натуральных чисел от 1 до n можно рассчитать по формуле S= 1/6*(2n + 1)*(n^2 + n). Пользуясь этой формулой, найди 2^2 + 3^2 + 4^2 + ... + 20^2.


Известно, что сумма квадратов последовательный натуральных чисел от 1 до n можно рассчитать по форму

Kseniya1521 Kseniya1521    3   07.01.2022 15:23    40

Ответы
4534567889246400607 4534567889246400607  07.01.2022 15:30

2869

Объяснение:

Необходимо найти сумму квадратов натуральных чисел до n=20, однако данная формула учитывает ещё и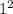 1^{2}, а в сумме, которую нужно найти, это слагаемое отсутствует, поэтому необходимо вычесть 1 из конечного результата

S=\frac{1}{6}(2n+1)(n^2+n)-1=\frac{1}{6}(2*20+1)(20^2+20)-1=\frac{1}{6}*41*(400+20)-1=\frac{41}{6}*420-1=2870-1=2869

ПОКАЗАТЬ ОТВЕТЫ
ноди1 ноди1  07.01.2022 15:30

ответ: 2869

Объяснение:

\displaystyle \rm S=\frac{(2n+1)(n+1)n}{6} 2^2+3^2+4^2+ \ldots +20^2=? S=\frac{(20\cdot 2+1)(20+1)20}{6} =\frac{41\cdot 21 \cdot 20}{6} = 2870 2^2+3^2+4^2+ \ldots +20^2= S-1^2=2870-1= 2869

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Алгебра
ania47 ania47  03.06.2019 07:20
На 100 грамм таблеток 260 калорий. сколько калорий в одной таблетке которая весит 0,5 ?...
moranikatya moranikatya  03.06.2019 07:20
Выполните действия ! b^2//5 : 7b//60y...
mailiiti63 mailiiti63  03.06.2019 07:20
1) cosx=0,6 2) cos x/2=-1 3) 2cos3x=-√3...
ms002 ms002  03.06.2019 07:20
Вшколе 36 первоклассников посещают группу продленного дня, что составляет 25% от общего числа всех первоклассников. сколько первоклассников учится в школе?...
OlgaBliznyak OlgaBliznyak  03.06.2019 07:20
Лене надо подписать 972 открытки ежедневно она подписывает на одно и то же количество больше по сравнению с предыдущим днем известно что за первый день лена подписала...
68Diman 68Diman  03.06.2019 07:20
1. записать с всевозможных равенств соотношение между x и y, если: 1) x больше y на 2: x-y=2 ? , ? , ? . 2) x меньше y на 5: ? , ? , ? . 3) x больше y в 3 раза: ? ,...
babaevgleb70 babaevgleb70  03.06.2019 07:20
Вкоробке четыре синих и восемь красных карандашей. наугад берут два карандаша. найдите вероятность того, что оба карандаша красные. ответ округлите до сотых....
FUNNIAO FUNNIAO  16.06.2019 20:40
Какое из следующих чисел является наименьшим? 1) 7,2*10(-50) 2)6,8*10(40) 3)6,9*10(-40) 4)9,1*10(-50)...
Ulugbek9i Ulugbek9i  16.06.2019 20:40
Функция задана формулой y= 4x -30 .определите а) значение y , если x =-2,5 б) значение x при котором y=-6 в) проходит ли крафик функции через точку b (7; -3)...
zligna zligna  16.06.2019 20:40
Пример уравнения вида х(в квадрате)=а,которое : 1.имеет два целых корня 2.не имеет корней. 3.имеет два рациональных корня 4.имеет два иррациональных корня....

Популярные вопросы