Известно что при некоторых натуральных значениях n значение выражения n³+n кратно 30. Будет ли кратно 30 при тех же значениях n значение выражения
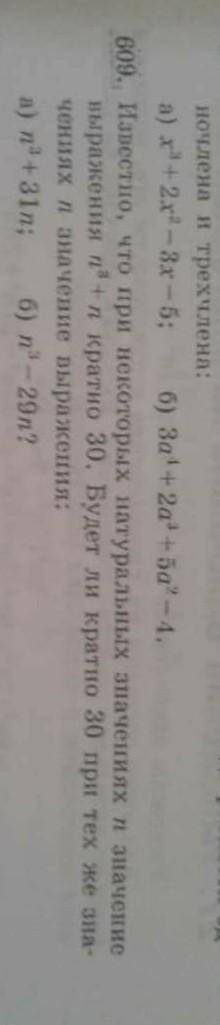
Другие вопросы по теме Алгебра
Популярные вопросы
- Розташуйте наведені дані алкени у ряд за збільшенням швидкості...
2 - Виберіть правильні твердження: Сучасні вчені поділяють прокаріотів...
3 - Масса 11,2л азота при н.у. равна а) 28г в) 24гб) 36г г) 14г...
3 - Установите тип словосочетания посуду по главному слову * наречное...
1 - Установите тип словосочетания я отличник по главному слову *...
3 - Таблица 8 класс Заполни таблицу, если плата за кВт*ч-2 рубля...
2 - (x+1)(x-2) (x+3)(x-4) Доведіть що для всіх значень х виконується...
1 - Хто зделает тут так мало украинцив До...
3 - Написать краткое изложение ...
1 - Немецкий А 2. Es ist hier zu kalt. Können Sie bitte die ......
1
Для начала, разложим число 30 на простые множители: 30 = 2 * 3 * 5.
Мы знаем, что если число кратно 30, то оно должно быть кратным каждому из этих простых множителей.
Разберемся по очереди с каждым из множителей.
1) Множитель 2: чтобы число было кратно 2, оно должно быть четным.
Проверим, будет ли n³+n четным при любом натуральном значении n.
Вспомним, что четное число делится на 2 без остатка.
Представим, что n равно 2k, где k — натуральное число. Тогда выражение n³+n можно записать как (2k)³+(2k).
(2k)³ = 8k³, а (2k) = 2k.
Сложим эти два выражения: 8k³+2k = 2(4k³+k).
Выражение 4k³+k является целым числом, поэтому результат выше также является четным числом.
Таким образом, выражение n³+n будет кратно 2 при любом натуральном значении n.
2) Множитель 3: чтобы число было кратным 3, сумма его цифр должна быть кратной 3.
Рассмотрим сумму цифр числа n³+n.
n³ — это число, полученное из числа n возводя его в куб.
Таким образом, сумма цифр n³ будет равна сумме цифр n+n+n.
А сумма цифр n равна самому числу n, поэтому сумма цифр числа n³+n равна 3n.
Таким образом, сумма цифр числа n³+n будет кратна 3 при любом натуральном значении n.
3) Множитель 5: чтобы число было кратно 5, оно должно заканчиваться на 0 или 5.
Рассмотрим последнюю цифру числа n³+n.
n³ — это куб числа n, поэтому последняя цифра числа n³ будет равна последней цифре числа n.
Таким образом, последняя цифра числа n³+n будет равна сумме последней цифры числа n и последней цифры числа n.
Последняя цифра числа n равна n, поэтому последняя цифра числа n³+n будет равна 2n.
Чтобы последняя цифра числа была 0 или 5, необходимо, чтобы 2n было кратно 5.
Кратность 5 достигается, когда n равно 5, 10, 15 и т.д.
Таким образом, последняя цифра числа n³+n будет кратна 5 при значениях n, кратных 5.
Итак, мы установили, что выражение n³+n будет кратно 2, 3 и 5 при любых натуральных значениях n.
Так как наше число должно быть кратным и 2, и 3, и 5 одновременно, оно должно быть кратным их наименьшему общему кратному.
НОК(2, 3, 5) = 30.
Таким образом, при всех натуральных значениях n выражение n³+n будет кратно 30.