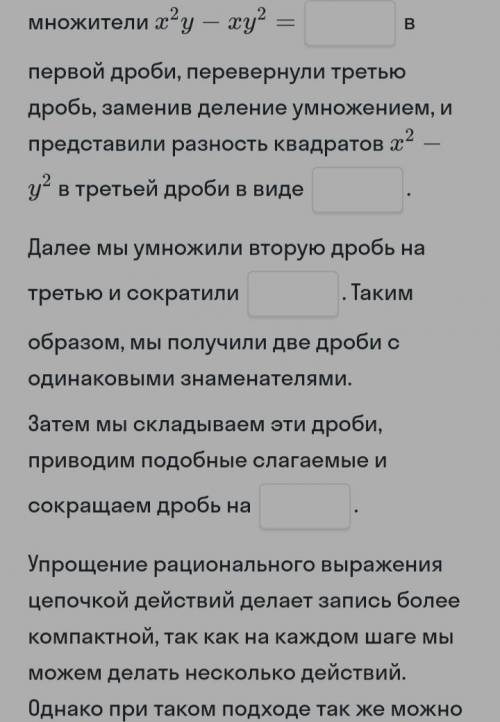
Изучи упрощение выражений цепочкой, заполняя пропуски

Для того, чтобы решить эту задачу, мы можем использовать некоторые основные правила упрощения алгебраических выражений. Давайте рассмотрим каждое выражение поочередно.

1) В первом выражении у нас есть сумма двух одночленов: 3x + 5x. Поскольку переменные (x) и степени (1) одинаковые, мы можем сложить коэффициенты (3 и 5) и оставить переменную без изменений. Получается: 3x + 5x = 8x.

2) Во втором выражении у нас также есть сумма двух одночленов: -7y - 2y. Мы можем сложить коэффициенты (-7 и -2) и оставить переменную без изменений. Ответ: -7y - 2y = -9y.

3) В третьем выражении у нас есть разность двух одночленов: 6a - 2a. Так как переменные (a) и степени (1) одинаковые, мы можем вычесть коэффициенты (6 и 2) и оставить переменную без изменений. Получается: 6a - 2a = 4a.

4) В четвертом выражении у нас также есть разность двух одночленов: 12b - 4b. Мы можем вычесть коэффициенты (12 и 4) и оставить переменную без изменений. Ответ: 12b - 4b = 8b.

5) В пятом выражении у нас есть сумма двух одночленов: m + 4m. Поскольку переменные (m) и степени (1) одинаковые, мы можем сложить коэффициенты (1 и 4) и оставить переменную без изменений. Получается: m + 4m = 5m.

6) В шестом выражении у нас также есть сумма двух одночленов: -2n - 6n. Мы можем сложить коэффициенты (-2 и -6) и оставить переменную без изменений. Ответ: -2n - 6n = -8n.

Таким образом, упрощение каждого выражения по цепочке дает следующие результаты:
1) 3x + 5x = 8x
2) -7y - 2y = -9y
3) 6a - 2a = 4a
4) 12b - 4b = 8b
5) m + 4m = 5m
6) -2n - 6n = -8n

Надеюсь, это помогло понять, как упростить выражения цепочкой. Если есть еще вопросы или что-то не ясно, пожалуйста, сообщите мне.