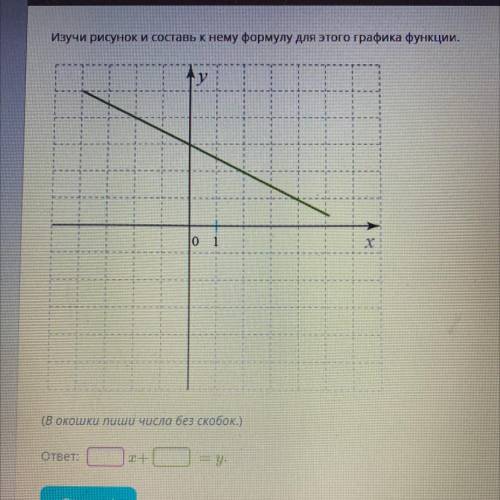
Изучи рисунок и составь к нему формулу для этого графика функции.

На данном графике изображена парабола, которая представляет собой график квадратичной функции. Квадратичная функция имеет общий вид f(x) = ax^2 + bx + c, где a, b и c - это коэффициенты, определяющие форму и положение графика.

Для того чтобы найти формулу для данного графика, нам необходимо определить значения коэффициентов a, b и c. Для этого мы можем использовать изображенные на графике точки. Данная парабола проходит через точку (0, -2), что означает, что при x = 0, значение функции равно -2. Используя это, мы можем найти значение коэффициента c.

В данном случае, значение c равно -2, так как это значение y, когда x = 0. Итак, наша формула принимает вид f(x) = ax^2 + bx - 2.

Теперь, чтобы определить значения коэффициентов a и b, мы можем использовать еще две точки на графике. На данном рисунке, эти точки можно считать (1, 0) и (-1, 0), так как они лежат как можно ближе к главной оси симметрии параболы.

Подставляя значения координат этих точек в нашу формулу, мы можем составить систему уравнений и решить её. Заметим, что в данных точках значение y равно 0, что значит, что f(1) = 0 и f(-1) = 0.

Подставим значения точки (1, 0) в формулу f(x):
0 = a(1^2) + b(1) - 2, или, более просто, a + b - 2 = 0.

Подставим значения точки (-1, 0) в нашу формулу f(x):
0 = a(-1^2) + b(-1) - 2, или, более просто, a - b - 2 = 0.

Итак, у нас получилась система уравнений:
a + b - 2 = 0
a - b - 2 = 0

Мы можем решить эту систему уравнений методом исключения или методом подстановки. Давайте воспользуемся методом исключения для получения значения коэффициента a.

Сложим наши уравнения:
(a + b - 2) + (a - b - 2) = 0 + 0

Упростим это выражение:
2a - 4 = 0

Теперь, добавим 4 к обеим сторонам уравнения и разделим на 2:
2a = 4
a = 2

Теперь, чтобы найти значение коэффициента b, мы можем подставить подсчитанное значение a в одну из наших исходных уравнений. Для этого, давайте воспользуемся уравнением a + b - 2 = 0.

Подставим значение a:
2 + b - 2 = 0

Упростим это выражение:
b = 0

Таким образом, мы нашли значения коэффициентов a и b. Значение коэффициента a равно 2, а значение коэффициента b равно 0.

И, в конечном итоге, формула для данного графика функции будет выглядеть следующим образом:
f(x) = 2x^2 + 0x - 2, или, проще говоря,
f(x) = 2x^2 - 2.