Изобразите на координатной плоскости множество решений системы неравенств
х²+у²≤9
у≤х+1
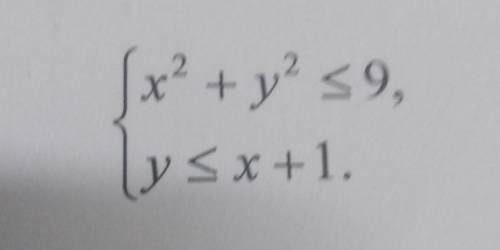
Другие вопросы по теме Алгебра
Популярные вопросы
- Джесси оуэнс – американский легкоатлет, завоевавший 4 золотых медали на олимпиаде...
1 - Выписать из сказок пушкина 2 предложения ссп и два предложения спп простые и сложные!...
1 - Вкакой четверти (окружности) находится промежуток от до...
1 - Урынын карама карсы созин айтындарш...
1 - Составьте уравнение реакций характеризующие свойства оксида серы(4)...
3 - 1)найти вес алюминевого кубика если его ребро равно 5 см 2) найдите вес тела, масса...
3 - Какие жанры относятся к необрядовой лирике? а) былины б) городской романс в) свадебные...
3 - Посадки леса занимают 420 га. ели занимают 63,5% этой площади, а сосны 29%.на сколько...
3 - Обьясните не с причастием эта (не) приятная надолго осталась в моей...
2 - Составте предложения. photos/like/taking/do/you 1. brother/part/is/the/match/in/going/to/football/take/my/...
3
Теперь посмотрим на второе неравенство: {у ≤ х + 1}. Оно представляет прямую с углом наклона 1 и смещением вверх на 1 относительно оси x.
Чтобы изобразить множество решений системы неравенств, нужно выбрать область, где пересекаются или перекрываются эти две фигуры.
Сначала нарисуем окружность x² + у² ≤ 9.
1. Начнем с центра окружности (0,0) и построим точку на радиусе, параллельно оси x. Радиус равен 3, поэтому эта точка будет (3,0).
2. Сделаем то же самое для радиусов, параллельных осям y, симметрично.
3. Проведем кривую линию через эти 4 точки для окружности.
Теперь построим прямую у = х + 1.
1. Найдем точку на оси у, где y равно 1. Эта точка будет (0,1).
2. Разберемся со скосом: если увеличиваем x на 1, то y также будет увеличиваться на 1. Нарисуем вторую точку параллельно оси x, с координатами (1,2). Всю прямую можно будет на них определить.
Теперь нарисуем систему неравенств на координатной плоскости.
Окружность будет закрашена, потому что неравенство говорит, что x² + у² должно быть меньше или равно 9. Кроме того, точки, находящиеся внутри окружности, также удовлетворяют у≤х+1.
Поэтому множество решений системы неравенств будет область, расположенная внутри окружности и выше прямой. Эта область будет закрашена на графике неравенств.
Область будет представлять собой полукруг с радиусом 3, ограниченный прямой y = x + 1. Получившаяся область можно увидеть на рисунке, который предоставлен.