Изобразите на координатной плоскости множество решений неравенства х²-2у-3> 3х

Ответы

саня9999999 08.10.2020 15:44

$x^2-2y-33x\\ \\ y$

Для начала построим обыкновенную параболу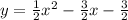 $y=\frac{1}{2}x^2-\frac{3}{2}x-\frac{3}{2}$ , а затем нарисуем область.

Графиком функции есть парабола, ветви которой направленны вверх.

Найдем ее координаты вершины параболы

$m=\dfrac{-b}{2a}=\dfrac{3/2}{2\cdot 1/2}=\dfrac{3}{2}$

$y=\dfrac{1}{2}\cdot \left(\dfrac{3}{2}\right)^2-\left(\dfrac{3}{2}\right)^2-\dfrac{3}{2}=-\dfrac{1}{2}\cdot \dfrac{9}{4}-\dfrac{3\cdot 4}{2\cdot 4}=-\dfrac{21}{8}$

Координаты вершины параболы: (3/2; -21/8)

Изобразите на координатной плоскости множество решений неравенства х²-2у-3> 3х

ПОКАЗАТЬ ОТВЕТЫ

Другие вопросы по теме Алгебра

LilyaDolz 14.04.2021 07:07

Вычитание алгебраических дробей Выполнить №463-465(1,3)1) 53ac+5ad3) c+5ad15aЗа 15а5b2+2b+3. 3) d3-cd+c2d21) 5b2+2b+3b2-b2a2-cdte2,d21) 9b2c+10a2d12a3b39b2c+10a2d12a3b33) 8х2-2y2+5xy12x2y3-8x2-2y2+5xy12x2y3...

фиаско123 14.04.2021 07:08

Cos100⁰cos110⁰+cos20⁰ cos10⁰...

ауе59 14.04.2021 07:08

575. Решите неравенство: а) (x-1)(х+3)(х-2)(х^2 + 1) 0;б) (x^2 - 5х + 6)(х^2 + 5х + 6) 0;в) (x^2 + 2х-3)(-2х^2 + 5x - 2) 0;г)(х + 2)(х + 5)(x-1)(х + 4) 0....

2006otvet 14.04.2021 07:10

Решите уравнение 6x - 8x² + 5 =0...

Ольдафіг 14.04.2021 07:10

с алгеброй нужно решить полностю без сокращённых видов...

MissRapunzel 14.04.2021 07:11

решить. Выполните действия....

msnyamkina 30.03.2021 11:37

Дана арифметическая прогрессия: 30; 24; 18;… Найдите сумму первых десяти ее членов...

DipperGo 30.03.2021 11:38

Направление электрического тока в витке показано на рисунке стрелкой. Определи направление линий магнитного поля в точке A. Из предложенных вариантов ответа выбери правильный:...

geamget 30.03.2021 11:38

ПАМАГИТЕ, КОНТРОЛЬНАЯ РАБОТА ПО АЛГЕБРЕ, ПЛЗ...

Йорик336 08.04.2020 12:58

3y^2 + 7y + 4 0; 9у^2 - 6у +1 0;3у^2-6у+3 0...

Изобразите на координатной плоскости множество решений неравенства х²-2у-3> 3х​

Популярные вопросы

Изобразите на координатной плоскости множество решений неравенства х²-2у-3> 3х