Из 8 мальчиков и 5 девочек надо выделить для работы на пришкольном участке 3 мальчиков и 2 девочек. Сколько существует?
Другие вопросы по теме Алгебра
Популярные вопросы
- От чего зависит распространение зон? 2.Чем отличается широтная...
2 - Какие устройства памяти являются встроенными какие - сменными?...
2 - 7/15+(x+1/20)x=23/56x если кому не понятно / это дробь...
3 - 2x²/х-7 = 7x-6/2-х Найдите корень уравнения...
2 - Рассчитайте количество теплоты, которое потребуется для нагревания...
2 - Сұрақтарға жауап беріңдер! Тараздың бойтұмарын анықтаңыз! Қарахан...
3 - План на древнегреческий миф Миф об аргонавтах ...
2 - Саундтрек, аниматор, картридж, каратист, гильдия, этикетка, клип...
1 - Реши систему уравнений методом подстановки:x−2y=−5 7x−9y=7...
3 - Терминов подберите соответствующие определения...
3
их число равно произведению числа сочетаний из 8 по три на число сочетаний из 5 по два, точнее 8!/(3!*5!))*(5!/(3!2!))=8*7*5*2=560
Найдём сначала девочек, затем мальчиков и перемножим их, это и будет нашим ответом:
1.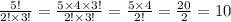 выбрать девочек;
выбрать девочек;
2.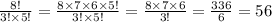 выбрать мальчиков;
выбрать мальчиков;
3.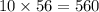 выбрать девочек и мальчиков вместе;
выбрать девочек и мальчиков вместе;
ответ: существует