Исследуйте на монотонность и экстремумы функцию f(x)=27 кубический корень x -x
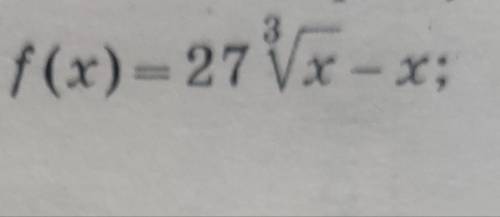
Другие вопросы по теме Алгебра
Популярные вопросы
- Какие страны входят в состав Восточной Европы Польша, Беларусь, Франция, Чехия,...
1 - Приведите пример моральной ответственности из жизни...
2 - У котрому рядку є числівники: * Сьогодні учень отримав двійку. Я прочитав багато....
3 - Выполните алгоритм,отображенный в виде блок-схемы,при различных значениях а,в,с....
2 - Дано: угол АВС=90°; АВ=5см; АС=13 см НАЙТИ: СД-?...
2 - 1) Какие задачи стояли перед новой династией во внешней политике с Речью Посполитой...
2 - При перетині двох паралельних прямих січною внутрішні різносторонні кути відносяться...
3 - Определи массу осадка, который образуется в реакции 180 г 10%-ного раствора хлорида...
3 - 1.Дана система двох лінійних рівнянь: {y+12x=2,3y−12x=4.Знайди значення змінної...
1 - ІВ. Напишіть будь- ласка одне із цих ЕСЕ: 1.Емігрант - зрадник чи патріот?(за...
3
Функция дана следующим образом: f(x) = 27√x - x
1. Найдем область определения функции:
У функции под знаком корня должно быть неотрицательное значение, поэтому x ≥ 0.
Таким образом, область определения функции: x ≥ 0.
2. Найдем производные функции:
Для исследования монотонности и нахождения экстремумов функции, нам необходимо найти производные первого и второго порядка.
Первая производная f'(x) позволяет определить, когда функция возрастает и когда убывает. Возьмем производную от каждого слагаемого в функции:
f'(x) = (27√x)' - x'
Для удобства дифференцирования вспомним, что √x = x^(1/2).
Тогда получим:
f'(x) = 27 * (x^(1/2))' - 1
Дифференцируем каждое слагаемое:
(x^(1/2))' = (1/2)x^(-1/2) = (1/2√x)
Теперь выразим первую производную:
f'(x) = 27 * (1/2√x) - 1
f'(x) = 27/2√x - 1
Вторая производная f''(x) позволяет определить, есть ли в точке экстремум и какого типа он будет:
f''(x) = (27/2√x - 1)'
Дифференцируем каждое слагаемое:
(27/2√x - 1)' = (27/2√x)' - 1'
Теперь найдем частные производные:
(√x)' = (1/2√x)
(1)' = 0 (производная постоянной равна нулю)
Теперь выразим вторую производную:
f''(x) = (27/2√x - 1)'
f''(x) = (27/2√x)' - 0
f''(x) = (27/2√x)
f''(x) = 27/(2√x)
3. Определение монотонности функции:
Для определения монотонности нужно проанализировать знак первой производной. Если производная положительна, функция возрастает, если отрицательна - функция убывает.
f'(x) = 27/2√x - 1
Установим неравенство нулю и найдем значения, где производная меняет знак:
27/2√x - 1 ≥ 0
27/2√x ≥ 1
27/2√x ≥ 2/2
27/2√x ≥ √x
Получаем неравенство:
√x ≤ 27/2√x
Теперь возводим обе части неравенства в квадрат:
(√x)^2 ≤ (27/2√x)^2
x ≤ (27/2)^2
x ≤ 27^2/4
x ≤ 729/4
Таким образом, итоговое множество, где функция возрастает или убывает, будет x ≤ 729/4.
4. Определение экстремумов функции:
Для определения экстремумов функции нужно проанализировать знак второй производной. Если вторая производная положительна, то в данной точке будет минимум, если отрицательна - будет максимум.
f''(x) = 27/(2√x)
Установим неравенство нулю и найдем значения, где производная меняет знак:
27/(2√x) > 0
27 > 0 (неравенство выполнено всегда)
Таким образом, функция f(x) не имеет экстремумов.
Итак, наше исследование показало, что функция f(x) = 27√x - x монотонно возрастает при x ≤ 729/4 и не имеет экстремумов.