Исследуйте функцию y=2-3x^2-x^3 на экстремум с решением
Ответы
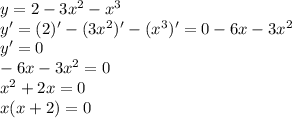
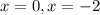 - экстремумы(точки минимума или максимума) функции.
- экстремумы(точки минимума или максимума) функции.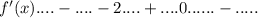
 - точка минимума.
- точка минимума.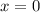 - точка максимума.
- точка максимума.
Другие вопросы по теме Алгебра
Популярные вопросы
- Как решить уравнение такого типа 10*(12+х)=500...
3 - Запиши кратко любым в столовую 2 мешка картофеля по 49 кг в каждом.часть...
2 - Тема время: сколько времени проходит: 1)с 5 ч вечера до 1 ч ночи, 2)с 3...
2 - Ликарь зробив щеплення учням. хлопчикам було 60а дівчаток було 20 меньше....
1 - Как решить в столбик пример 963×407...
1 - Начерти прямоугольник, длина которого равна 6 см, а ширина в 3 раза меньше....
1 - 1)вместо * в формуле линейной функции составьте такое число, чтобы графики...
2 - Как не путаться что бы правильно написать грохочут или грохочат поезда?...
2 - 3предложения с указазательными местоимениями и фразиалагизм...
1 - Из городов а и в, расстояние между которыми 108 км навстречу друг другу...
3