Исследуйте функцию f(x) = 3x^4 + 4x^3 - 12x^2 + 12 и постройте её график. найдите количество корней f(x) = a для каждого действительно значения параметра а.
Другие вопросы по теме Алгебра
Популярные вопросы
- Из 5 кг.хлопка можно изготовить 100 м. батистовой ткани. сколько надо...
3 - Встоловую 5 мешков риса по 24 кг в каждом и пшено. пшено в 3 раза больше,чем...
2 - Напиши сочинение 5-7 предложений на тему 9 мая день победы .чем важен...
2 - Толкование лексического значения слов: клен, осина, береза, дуб....
1 - Умоем кормане 40 копеек половина денег у меня монетами по 5 копеек а остальные...
3 - Он бестрашно(морфемный разбор) ходил(морфологический разбор) ночью(фонетический...
1 - Нужно ! выражение ( -2x³y)³×(-5x²y)²...
3 - Красная лента на 7 дм длиннее, чем белая, а зеленая лента на 10 дм длиннее,...
2 - Вкаком году был издан судебник ивана3...
1 - Вырози 7м5см =см 2ч=мин 3дм 6см= 3ч 15мин=минут 40дм=м 2сут=ч 52мм=см...
1
1. Область определения функции: множество всех действительных чисел.
2. Функция не периодическая.
3. Проверим на четность или нечетность функции:
Функция является ни четной ни нечетной.
4. Точки пересечения с осями координат:
4.1. Точки пересечения с осью абсцисс(y=0).
4.2. Точки пересечения с осью ординат(x=0):
Раз х=0, то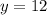
5. Точки экстремума, возрастание и убывает функции.
Приравниваем теперь производную функции к нулю, имеем:
Произведение равно нулю, если хотя бы один из множителей равен нулю.
____-___(-2)___+__(0)__-____(1)___+___
Функция возрастает на промежутке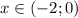 и
и 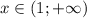 , а убывает -
, а убывает - 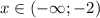 и
и 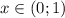 . Производная функции в точке х=-2 и х=1 меняет знак с (-) на (+), значит точка х=-2 и х=1 являются точками локального минимума. А в точке х=0 производная функции меняет знак с (+) на (-), следовательно, точка х = 0 - локальный максимум.
. Производная функции в точке х=-2 и х=1 меняет знак с (-) на (+), значит точка х=-2 и х=1 являются точками локального минимума. А в точке х=0 производная функции меняет знак с (+) на (-), следовательно, точка х = 0 - локальный максимум.
6. Точки перегиба
На промежутке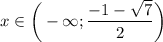 и
и 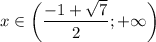 функция выпукла вниз, а на промежутке
функция выпукла вниз, а на промежутке 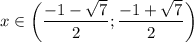 - выпукла вверх.
- выпукла вверх.
Вертикальных, горизонтальных и наклонных асимптот нет.
Теперь найдем количество корней f(x)=a для каждого действительно значения параметра а.
f(x)=a - прямая, параллельная оси абсцисс.
При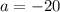 уравнение будет иметь один корень.
уравнение будет иметь один корень.
При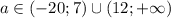 уравнение имеет два корня.
уравнение имеет два корня.
При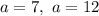 уравнения имеет три корня
уравнения имеет три корня
При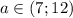 уравнение имеет четыре корня.
уравнение имеет четыре корня.