Исследуйте функцию F(x)=2/3x^3+4x^2-10 на экстремумы
Другие вопросы по теме Алгебра
Популярные вопросы
- 1 What was the weather like?A2 Where did Gulsara...
3 - Read the text again and write next to the sentences True or False according...
3 - B. Вспомни, что такое перифраз. Приведи примеры перифраза из прочитанного отрывка...
1 - Задание №1. Прочтите текст, определите и запишите открытую и скрытую (подтекст)...
1 - Кто так в Word-де сделать? по быстрому...
1 - Дано вектор а (6;-3).Знайдіть координати вектора 1)2a 2)-a 3)1/3 a...
1 - А) Если опустить мрамор в азотную кислоту происходит выделение газа. Запишите...
3 - Развитие спутниковой связи за и против...
2 - Определи события из истории Могулистана. ...
2 - Заполните пропуски в тексте. К Первой мировой войне привели противоречия между...
1
Функция достигает наименьшего значения -10 при x = 0.
Функция достигает наибольшего значения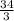 при x = 4.
при x = 4.
Объяснение: