1. Алгебра
  2. Исследовать знакопеременный

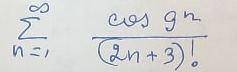
Исследовать знакопеременный ряд на абсолютную и условную сходимость


Исследовать знакопеременный ряд на абсолютную и условную сходимость

Юлья0000000 Юлья0000000    3   20.10.2020 00:04    0

Ответы
dinagasanova12 dinagasanova12  19.11.2020 00:06

\sum \limits _{n=1}^{\infty }\, a_{n}=\sum \limits _{n=1}^{\infty }\dfrac{cos\, 9^{n}}{(2n+3)!}\\\\\\\sum \limits _{n=1}^{\infty }\, |\, a_{n}\, |=\sum \limits _{n=1}^{\infty }\dfrac{|\, cos\, 9^{n}\, |}{(2n+3)!}\\\\\\\dfrac{|\, cos\, 9^{n}\, |}{(2n+3)!}\leq \dfrac{1}{(2n+3)!}\ \ \ ,\ \ \ \ \sum \limits _{n=1}^{\infty }b_{n}=\sum \limits _{n=1}^{\infty }\dfrac{1}{(2n+3)!}\ -\ sxoditsya\ ,\ tak\ kak

po\ priznaky\ Dalambera\\\\\lim\limits _{n \to \infty}\dfrac{b_{n+1}}{b_{n}}=\lim\limits _{n \to \infty}\dfrac{1}{(2n+5)!}:\dfrac{1}{(2n+3)!}=\lim\limits _{n \to \infty}\dfrac{(2n+3)!}{(2n+5)!}=\\\\\\=\lim\limits _{n \to \infty}\dfrac{(2n+3)!}{(2n+3)!\cdot (2n+4)(2n+5)} =\lim\limits _{n \to \infty}\dfrac{1}{(2n+4)(2n+5)}=0

Сходится мажорантный ряд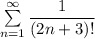   \sum \limits _{n=1}^{\infty }\dfrac{1}{(2n+3)!}   , значит по признаку сравнения сходится и минорантный ряд  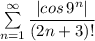   \sum \limits _{n=1}^{\infty }\dfrac{|cos\, 9^{n}|}{(2n+3)!}   -  ряд,

составленный из абсолютных величин исходного ряда.

Из сходимости ряда из абсолютных величин следует  абсолютная

сходимость исходного ряда .

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Алгебра
DaniilPedrol DaniilPedrol  02.09.2019 17:00
Вмешке у деда мороза осталось 70 яблок и 20 груш, какова вероятность того, что из мешка достанут яблоко? ответ укажите с точностью до 0,01...
моллск моллск  02.09.2019 17:00
Решите пример решите уравнение (x+3)^4+2(x+3)^2-8=0 он из второй части, разберите...
08122005vlad 08122005vlad  02.09.2019 17:00
Вкаждом купе вагона поезда 4 места. какой номер купе, где едит пасажир с номером места 17...
nargis1077 nargis1077  02.09.2019 17:00
двоє робітників можуть виконати роботу за 10 днів. після 7 днів спільної роботи один з них захворів, і другий закінчив роботу, пропрацювавши ще 9 днів. за скільки днів кожен...
svyatoslavkorchagin svyatoslavkorchagin  02.09.2019 17:00
Сравните корень из 9+2 корня из 5* корень из 9-2 корня из 5 и 7,9...
medinceva24674qq medinceva24674qq  02.09.2019 17:00
Определите, какая из функций y=3x-4. y= корень x+3. y=x^2+3x-4. y=x+3 является квадратичной?...
gadukina gadukina  02.09.2019 17:00
Постройте график функции y=|x-1|-|x+2| и определите, при каких значениях k прямая y=kx имеет с графиком ровно одну общую точку...
лцстцлстлцс лцстцлстлцс  02.09.2019 17:00
Втреугольнике abc угол c равен 90°, ab = 50, sin a = 24/25. найдите ac....
dwinchester15 dwinchester15  02.09.2019 17:00
4sin (п/2+ a)+ cos (п-a), если cos a=-0,9...
visor0304 visor0304  14.06.2020 20:30
Сравните значения выражений 37⁹ и 2¹⁸×3¹⁸...

Популярные вопросы