Исследовать сходимость рядов по интегральному признаку
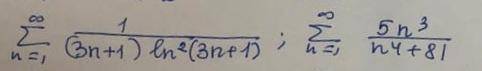
Другие вопросы по теме Алгебра
Популярные вопросы
- До школи завезли картоплі у 3 рази більше ніж моркви .а капусии на 177 кг...
1 - Дан массив из 11 случайных, целых чисел, заданных на интервале [0,10]. сдвинуть...
3 - Измерь стороны четырехугольников. найди их площадь и периметр...
2 - Проект по языку 4 класс my day on weekdays i get up first, then after that...
3 - Это сложно, , сделайте кто сколько сможет, умоляю ! 1.0,5(5x−5) (раскрыть...
2 - 47*x=282 x-это неизвестное число *- это умножение...
1 - Мне нужно 2 сложносокращённых слов !...
3 - Выскажите предположение: что будет, если прекратится обмен веществом (энергией,...
1 - Дан угол. определить в какой четверти он находится(дайте формулы)...
1 - Даны координаты вершин треугольника ab: a(-6; 1)b(2; 4) c(2; -2).докажите,что...
3
1) ряд сходится
2) ряд расходится
Объяснение:
Для первой суммы рассмотрим интеграл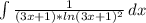
Он равен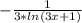 . При
. При 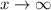 знаменатель дроби стремится к бесконечности, дробь стремится к нулю. Значит первый ряд сходится.
знаменатель дроби стремится к бесконечности, дробь стремится к нулю. Значит первый ряд сходится.
Для второй суммы рассмотрим интеграл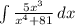
Он равен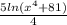 ,
, 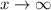 выражение стремится к бесконечности. Значит второй ряд расходится.
выражение стремится к бесконечности. Значит второй ряд расходится.