Исследовать на сходимость ряд 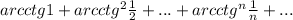
Другие вопросы по теме Алгебра
Популярные вопросы
- For each question, choose the correct letter A, B, C or D. 1 What is...
2 - Соедини картины с видами вышивки ...
1 - Мәтіндегі ойға сатысты өз пікірлерінді «попс формуласы бойынша далелдендер...
3 - Тема: Отрар дать описание по дескриптору.дескп.: дает общее опсание...
2 - За правилами дорожнього руху, гальмівна система автомобіля вважається...
3 - Арифметические действия над рациональными числами. урок...
3 - Батьківщина заповіту текст потрібно...
2 - в равнобедренном треугольнике ABC (AB = BC) периметр которого равен...
3 - Полагает, что существо, к которому обращаются с «зовом, может Прочитайте...
3 - Ha pune. 4 AP12, NK =*, PK-9. Anar AN.AIB...
2
Объяснение:
Когда мой друг сказал. " пацаны расходимся" этот ряд тоже пошёл. дело в том что чем больше n. тем ближе аргумент котангенса к нулю. А при Х стремящимся к 0. ctg(X) стремится к бесконечности. + ты ещё в степень возводишь. расходится
Объяснение:
Заметим, что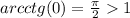 . Так как
. Так как 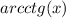 непрерывен в нуле, то существует
непрерывен в нуле, то существует 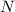 , что для любых
, что для любых