Исследовать на экстремум функцию y=x^3+3x^2+9x-6
Ответы
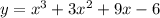 Найдем производную функции:
Найдем производную функции: 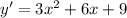 . Теперь приравняем производную к нулю, чтобы найти точки экстремума:
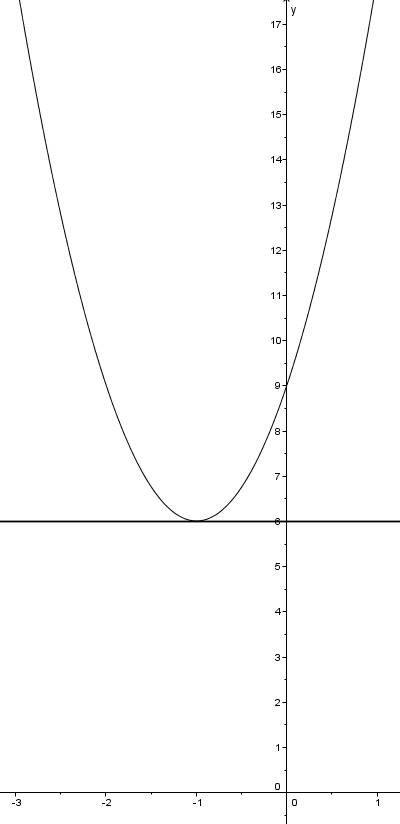
. Теперь приравняем производную к нулю, чтобы найти точки экстремума: 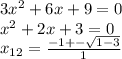 . Как видно, дискриминант квадратного уравнения отрицательный, а значит решений нет, отсюда заключаем, что точек экстремума у данной функции нет! (Во вложениях изображение производной!)
. Как видно, дискриминант квадратного уравнения отрицательный, а значит решений нет, отсюда заключаем, что точек экстремума у данной функции нет! (Во вложениях изображение производной!) 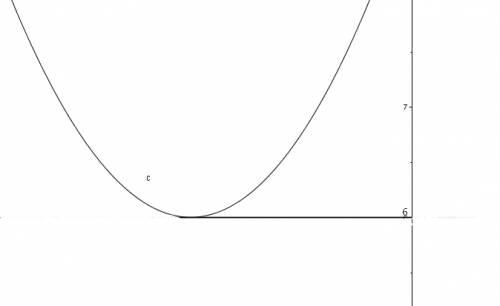
Другие вопросы по теме Алгебра
Популярные вопросы
- Аннотация к произведению сергея алексеевича лиепая...
3 - Решите уравнение х²+у²-12x+4y+40=0....
2 - Основным элементом любого организма является : 1)водород 2)углерод...
1 - Напишите сочинение на тему “экскурсия по современным чудесам света”...
1 - Твір на тему яка байка леоніда глібова найбі 20 ів...
2 - 30 выписать 5 предложений из худож. (использование авторских знаков)...
3 - Мы ощущаем в музыке не только мир,в котором жили люди до нас ,но,словно...
1 - Реферат по музыке 6 класс тема жанры народной музыки...
2 - Переведите на казахский без переводчика . бабушка . все бабушки...
1 - 7x+2y=9 5x+2y=11 решите подстановкой...
3