1. Алгебра
  2. Исследовать функцию

Исследовать функцию на монотонность


Исследовать функцию на монотонность

akon1708 akon1708    2   27.06.2020 06:01    0

Ответы
Renavalion Renavalion  06.09.2020 23:53

Функция монотонно возрастает на промежутках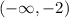 (-\infty, -2)

и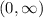 (0, \infty)

Функция монотонно убывает на промежутке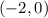 (-2,0)

Объяснение:

Как известно, монотонность зависит от знака производной: если производная < 0, то функция монотонно убывает, если > 0, то возрастает.

Найдем же её (производную):

y^\prime = (x^3 + 3x^2 + 4)^\prime = 3x^2 + 6x = 3x(x + 2). Пользуясь методом интервалов, получаем, что

y^\prime < 0 на промежутке (-2, 0)

y^\prime 0 на промежутках (-\infty, -2), (0, \infty)

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Алгебра
sakds sakds  21.07.2019 21:01
Разложите на множители: а)49-а² б)-0,01x²+b² в)y³+1000...
Rozeta2003 Rozeta2003  21.07.2019 21:00
Найти значение a при которых уравнение ax^2-3x+2=0 не имеет корней...
Елена060720007 Елена060720007  21.07.2019 21:00
Формулы сокращённого умножения напишите !...
kristinkadulesova kristinkadulesova  18.02.2021 08:08
Вычислить: 6sin230° – 6cos2⁡30°....
aimnura73 aimnura73  18.02.2021 08:06
Вы даете фору своему другу и начинаете бежать одновременно в одном направлении. Между вами расстояние 90м. Ваша скорость 2 м/с а у друга 1,5 м/с. Через какое время вы догоните друга?...
Privet34522 Privet34522  15.09.2019 21:00
1) найти произведение корней уравнения x^2-5x+6=0 и сравнить его со свободным членом уравнения. 2) найти сумму корней уравнения x^2-5x+6=0 и сравнить её со вторым коэффициентом...
neznaika168 neznaika168  15.09.2019 21:00
Селькохозяйственная культура , выращиваемая на чеках: а) рожь; b) хлопчатник; с) арбузы; d) свекла; е) рис кто знает, ! )...
mila7772 mila7772  15.09.2019 21:00
X^2+15x^2+50 уравнения приводящиеся квадратным решить...
илья33567б0 илья33567б0  15.09.2019 21:00
Сократить дробь: 1) (2x+1)*(x+3) 2) (1-3x)*(x+2) дробная черта дробная черта (3+x)8*2x (x-3)*(3x-1) за ответ 60 !...
vadimkamazurke vadimkamazurke  15.09.2019 20:50
Две машинистки перепечатали часть рукописи за 2 ч а затем первая машинистка за 1 ч самостоятельно закончила работу за сколько часов первая машинистка самостоятельно перепечатала...

Популярные вопросы