Исследовать функцию и построить график.
Другие вопросы по теме Алгебра
Популярные вопросы
- Вкаком ряду пропущены буквы только в словах с чередующейся гласной корня ? 1) ,...
2 - Почему безударную гласную в слове надо проверять...
3 - Путешествие от углича по волге на катере в первый день проплыли 72 км во второй...
3 - Найдите нок чисел: а) 63 и 129 б) 75 и 240 поехали!...
1 - Почему мы считаем что зародилась от шумеров?...
3 - Периметр треугольника oab равен 59 см. сторона оа равна 25см, а разность сторон...
2 - Причины военных успехов арабов в 8 веке....
1 - Найди объем фигуры,в которой прорезали сквозное отверстие.длина 5см,ширина5см,высота3...
2 - Выражение и найдите его значение. -6 × (0,5 × 2/3-1,5)-4,5×2/3 -8...
2 - Текст на тему its my ! ! багато ів, . 25б...
2
1. Область определения:
x∈(-∞;-1)∪(-1;2)∪(2;+∞)
2. Функция общего вида.
3. Найдём точки пересечения с осями:
4. Исследование с первой производной:
Cм. внизу.
5. Исследование с второй производной:
Выражение в скобках в числителе всегда положительное и не равняется нулю, см. внизу.
6. Уравнение асимптот:
Уравнения наклонных асимптот обычно ищут в виде y = kx + b. По определению асимптоты: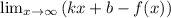
Находим коэффициент k: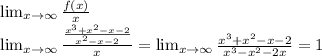
Находим коэффициент b: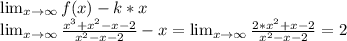
Получаем уравнение наклонной асимптоты: у=x+2
Найдем вертикальные асимптоты. Для этого определим точки разрыва: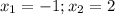
Находим переделы в точке x=-1
Это точка разрыва II рода и является вертикальной асимптотой.
Находим переделы в точке x=2
Это точка разрыва II рода и является вертикальной асимптотой.