Исследовать функцию и построить ее график f(x)=x^3-3x
Другие вопросы по теме Алгебра
Популярные вопросы
- Составьте формулы карбоновых кислот по названию 2 метилбутановая...
3 - Число всех атомов элементов в оксиде марганца (7) равно 1) 2; 2)...
1 - На стройку дома 45 ванн 5 часть всех вам установили в квартирах первого...
3 - Complete the sentences. choose the right form. a) my parents /were...
2 - Длина окружности, вписанного в правильный треугольник, равна 2 см....
2 - Водном из ниже предложений неверно употреблено выделенное слово....
2 - Как изменяется температура воздуха в течении суток....
2 - Bilden sie satze nach dem muster: 1)hans, rolf, weit, wohnen. 2)...
3 - Площвдь прямоугольника 120см 2.найди длиеу и ширину прямоугольника...
1 - Уживотного 6 ног,тело разделено на голову,грудь и брюшко.это?...
2
Области определения и значений все числа.
Функция нечётная т.к. f(x)= -f(-x)
Найдём точки пересечения с осями координат.
Найдём промежутки возрастания, убивания и экстремумы функции.
Смотри внизу.
Найдём координаты min и max.
Найдём точки перегиба.
Соответственно 0 это точка перегиба x<0 функция выпукла вверх
x>0 функция выпукла вниз.
Координаты точки перегиба: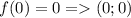
Можем строить график функции.