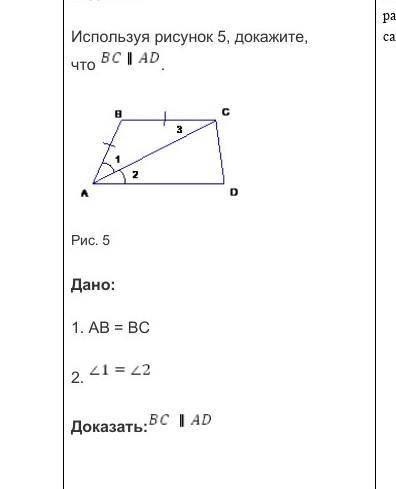
Используя рисунок 5, докажите, что . BC//AD

Рис. 5

Дано:

1. AB = BC

2. угол1=углу2

Доказать: AB=BC

​

Приветствую! Для доказательства того, что BC параллельно AD, мы можем использовать свойства параллельных линий и треугольников с равными углами.

В данном случае, у нас имеется треугольник ABC, в котором AB = BC (№1 в дано). Также, согласно данным у нас есть два равных угла, угол1 и угол2.

Наша цель - показать, что BC // AD, что означает, что линия BC параллельна линии AD.

Для этого мы можем использовать свойство параллельных линий, которое гласит, что если у нас есть две линии, и на них лежат пересекающиеся друг с другом попарно углы их прямолинейных высот, и эти углы равны, то эти линии параллельны.

Давайте воспользуемся этим свойством и рассмотрим прямую высоту H нашего треугольника ABC.

Так как AB = BC (№1 в дано), а угол1 = угол2 (№2 в дано), мы можем заключить, что треугольник ABC является равнобедренным треугольником.

Следовательно, прямая высота H, проведенная из вершины C к основанию AB, будет делить основание AB пополам. То есть, H делит AB на две равные части.

Из данного следует, что треугольники AHC и BHC равны между собой по двум сторонам и одному углу, и, следовательно, он будет равен третьему углу.

Поскольку треугольники AHC и BHC имеют два равных угла и сторону HC общую, они являются равными треугольниками.

Таким образом, сторона AH равна BH (по свойствам равных треугольников). Но это означает, что линии AD и BC (т.к. этот отрезок пересекает прямую высоту H в его середине) параллельны.

Таким образом, мы доказали, что BC // AD, с использованием свойств параллельных линий и равных треугольников.