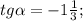Используя определение тангенса и котангенса произвольного угла, найдите tga и ctg а, если известно, что точка Р. единичной окруж- ности имеет координаты: б) Рª (15/17;-8/17); б.) Pª (0,6;-0,8)
Другие вопросы по теме Алгебра
Популярные вопросы
- Сколько фотонов испускает лампа мощностью 90 вт за 1 секунду...
2 - Годы правления , основные направления деятельности, владимир...
2 - Определите классы соединений,дайте названия веществ,формулы...
1 - Какому из перечисленных растений требуется больше всего света...
1 - Не приводя к общему знаменателю определи какая из них меньше:...
2 - Складіть і запишіть діалог (6-7 реплік) на тему погода . використайте...
3 - Выполни действия: 2,3+1,4 полученный результат проверь сложением...
2 - Решить прямоугольный треугольник ,катеты которого равный 4 и5...
2 - Чем кап (нарост на дереве) опасен для деревьев?...
2 - Какая статья за то, что мне надоело что откудато у меня берут...
3
а) =>
=> 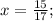
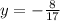
ответ: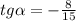
б) =>
=> 
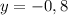
ответ: