Популярные вопросы
- Найдите значение выражения: 1/5 * 5,5 + (3/10 - 3)...
2 - 4класс: - площа прямокутника 640м квадратних,а довжина сторони 40м.знайти площу...
3 - Допиши вместо точек подходящее слово! сложная тяжелая грустная яркая лучшая...
2 - Какую функцию выполняет корневой вырост на нижнем конце стебля?...
3 - Два тела, имеющие равные положительные заряды, отталкиваются в воздухе с силой...
3 - Выберите из перечисленных растений семейства сложноцветные: тысячелистник, пижма...
3 - Написать сочинение на тему: характеристика тараса бульбы...
3 - Может ли быть в художественном произведении несколько сюжетов...
3 - Давление 800h/см квадрат площадь 40 мм квадрат найти силу система си 800h/см...
3 - Ведущими отраслями сельского хозяйства европейского севера являются: а) оленеводство,...
2
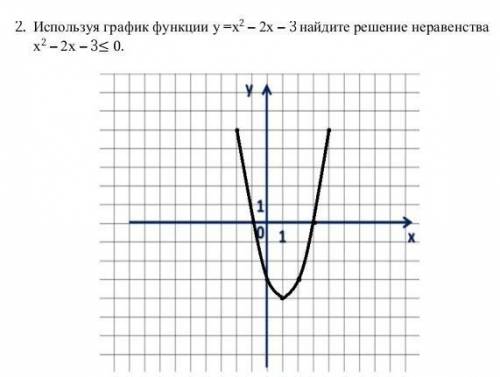
В решении.
Объяснение:
Используя график функции у = х² – 2х – 3 найдите решение неравенства
х² – 2х – 3 ≤ 0.
Приравнять к нулю и решить квадратное уравнение:
х² – 2х – 3 = 0
D=b²-4ac = 4 + 12 = 16 √D=4
х₁=(-b-√D)/2a
х₁=(2-4)/2
х₁= -2/2
х₁= -1;
х₂=(-b+√D)/2a
х₂=(2+4)/2
х₂=6/2
х₂=3.
Уравнение квадратичной функции, график - парабола, ветви направлены вверх, пересекают ось Ох в точках х= -1 и х= 3.
Решение неравенства: х∈[-1; 3].
Неравенство нестрогое, скобки квадратные.