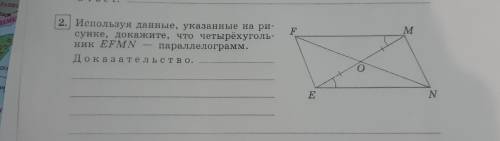
Используя данны, указанные на рисунке, докажите что четырёхугольник EVEN параллелограмм . доказательство.

Для того чтобы доказать, что четырехугольник EVEN является параллелограммом, мы должны использовать данные, указанные на рисунке и применить определение параллелограмма.

Определение параллелограмма гласит, что четырехугольник является параллелограммом, если его противоположные стороны параллельны и равны по длине.

На рисунке мы видим следующее:
1. Сторона VE параллельна и равна стороне EN (это следует из того, что обе стороны вертикальны и обозначены одним и тем же значком).
2. Сторона NE параллельна и равна стороне EV (это также следует из того, что обе стороны вертикальны и обозначены одним и тем же значком).
3. Сторона EN равна стороне NV (это является прямым следствием того, что сторона NE параллельна и равна стороне EV).
4. Сторона VE равна стороне EV (это является прямым следствием того, что сторона VE параллельна и равна стороне EN).

Таким образом, мы имеем стороны VE, EN, NE и EV, которые параллельны и равны по длине. Следовательно, по определению параллелограмма, четырехугольник EVEN является параллелограммом.