1. Алгебра
  2. Иррациональное уравнение ;

Иррациональное уравнение ; корень ха квадрате -9+корень2х+3=3


Иррациональное уравнение ; корень ха квадрате -9+корень2х+3=3

ромашка261 ромашка261    2   25.10.2020 01:24    7

Ответы
Kachmaresghg Kachmaresghg  12.02.2021 13:49

(см. объяснение)

Объяснение:

\sqrt{x^2-9}+\sqrt{2x+3}=3

Введем функцию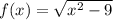 f(x)=\sqrt{x^2-9}.

Найдем D(f):

x^2-9\ge0\\x\in(-\infty;\;-3]\cup[3;\;+\infty)

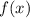Т.к. корень не меняет монотонность функции, то на промежутке (-\infty;\;-3] функция f(x) убывает, а на промежутке 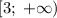[3;\;+\infty) возрастает.

Введем функцию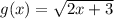 g(x)=\sqrt{2x+3}.

g(x) монотонно возрастает на промежутке x\in\left[-\dfrac{3}{2};\;+\infty\right).

Т.к. все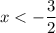 x  не подходят по ОДЗ для 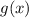g(x), а часть функции 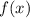f(x), определенная на промежутке 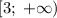[3;\;+\infty), возрастает, то имеем сумму возрастающих функций, а значит m(x)=\sqrt{x^2-9}+\sqrt{2x+3} возрастающая.

Значит уравнение m(x)=3 имеет единственный корень.

Предположим, что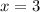 x=3 - корень уравнения.

Проверим это:

\sqrt{3^2-9}+\sqrt{2\times3+3}=3\\0+3=3

3=3, верно.

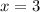Значит x=3 - это корень исходного уравнения.

Поэтому правильный ответ на задание 3) 3.

Уравнение решено!

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Алгебра
Bogdan8ra4yk Bogdan8ra4yk  23.08.2019 20:50
Решите систему сложения 4(x+1)-2(y+5)=1 5(7-x)+4(y-2)=10...
кириешка5 кириешка5  23.08.2019 20:50
Сможете - в таблице представлена урожайность зерновых культур в россии в 1992-2001 гг. год 1992 ц/га- 18,0. год 1993 ц/га -17,1. год 1994 ц/га 15,3. год 1995 ц/га - 13,1. год 1996...
MariaVay000 MariaVay000  23.08.2019 20:50
Решить систему уравнений. x − 2y = 4, x^2 + y^2 = 37....
nosorpg02 nosorpg02  23.08.2019 20:50
Решить в целых числах уравнение 3^y=x ^2-8x+7...
Lizzkkaa Lizzkkaa  23.08.2019 20:50
Надо найти последнюю цифру числа 13 в 2016 степени...
borisrrvdow9kk7 borisrrvdow9kk7  13.08.2019 23:30
Обчислити. sinп/8cosп/8 якшо не ясно це сінус помножити на пі поділити на 8 дробом і помножити на косинус помножити на піі поділити на вісім дробом іть пліз...
Matvey1745789 Matvey1745789  13.08.2019 23:30
Найдите значение выражения 6,1 ✖ 8,3- 0,83...
nikputen1 nikputen1  13.08.2019 23:30
1)цена билета в театр выросла на 40 %а выручка снизилась на 16 %на сколько %уменьшилось число зрителей? 2) 2 автомобиля двигаются вдоль одной прямой скорости автомобилей относительно...
zoeves zoeves  13.08.2019 23:30
Объясните как решать такие примеры 3x-9 = 0 2-x...
милашка357 милашка357  13.08.2019 23:30
Зная, что f(x)=√x, реши уравнение f(x−2)=46....

Популярные вопросы