Интересная задачка...
Только вот как это доказать

Другие вопросы по теме Алгебра
Популярные вопросы
- Опис історичної події з історії вс. 11 клас...
1 - Для внутрішніх районів Євразії, віддалених від усіх океанів, характерним...
2 - История России 10 класс 1. Подтвердите фактами или опровергните мнение:...
2 - 1. Хранителем наследственной информации являются А) рибосомы В) хромосомы...
1 - Схема образования водородной связи ...
3 - Решить неравенства, изобразить решение неравенств на числовой прямой...
2 - ЧЕНЬ ЗАРАНИЕ Сформулировать и аргументировать выводы о значении личности...
1 - Складіть рівняння реакції за до яких можна здійснити перетворення 1.в...
2 - Экономика, Задание : Найдите соответствия. Тема: Государственный бюджет....
3 - Для води характерні такі властивості, якА взаємодія з неметаламиБ взаємодія...
1
Пусть известно число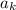 , оценим
, оценим 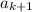 . Тогда достаточно выкинуть из всевозможных слов длины
. Тогда достаточно выкинуть из всевозможных слов длины 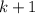 слова, начинающиеся со слов длины
слова, начинающиеся со слов длины 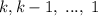 (таковых
(таковых 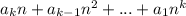 ), то есть
), то есть 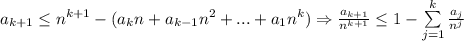 . Отсюда
. Отсюда 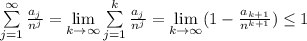 , поскольку очевидно, что
, поскольку очевидно, что 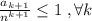 , ведь максимальное число слов длины
, ведь максимальное число слов длины 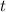 есть число
есть число