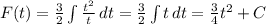Интеграл от 0 к 3.5(подинтегральное уравнение dx/корень кубический с 2x+1)
Другие вопросы по теме Алгебра
Популярные вопросы
- Запишите в виде натурального числа: 1,25 млн= 0.7тыс=...
1 - Футболист пробежал по полю на север 40 м затем 10 м на восток потом...
2 - Построить в тетради квадрат со стороной 2 см и найти его периметр...
2 - Составить сложное предложение с словами (путешествовать, водопад,лесоруб))...
2 - Представьте дроби в виде смешанного числа: 435 45-ых,793 38-ых,389...
3 - Напишите уравнение реакции взаимодействия бутена-1 с бромоводородом....
3 - Федор решил 3 ,это на 2 меньше,чем решила лена,а афанасий решил на...
2 - Под действием силы 20 н тело приобретает ускорение 0,5 м/с в кв чему...
1 - Что выделяют из попутного нефтяного газа? где используют?...
3 - Какого изменение импульса бегуна массой 60 кг,увеличевшего свою скорость...
2
Делаем замену перменной
Тогда