1. Алгебра
  2. Интеграл от 0 до п cos(2п/3 -

Интеграл от 0 до п cos(2п/3 - 3x) dx. нужно найти первообразную и потом подставить интеграл от 0 до п

GiTToS GiTToS    2   04.07.2019 16:10    2

Ответы
Андрей1щщщщз Андрей1щщщщз  02.10.2020 20:06
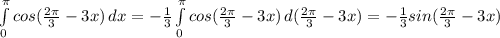\int\limits^ \pi _ 0 {cos( \frac{2 \pi }{3}-3x) } \, dx =- \frac{1}{3} \int\limits^ \pi _ 0 {cos( \frac{2 \pi }{3}-3x) } \, d( \frac{2 \pi }{3}-3x)=- \frac{1}{3} sin( \frac{2 \pi }{3}-3x) тут верт. 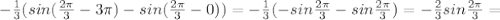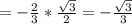черта и пределы и границы пишутся =- \frac{1}{3}(sin( \frac{2 \pi }{3}-3 \pi )-sin( \frac{2 \pi }{3}-0))=- \frac{1}{3} (-sin \frac{2 \pi }{3}-sin \frac{2 \pi }{3})=- \frac{2}{3} sin \frac{2 \pi }{3}==- \frac{2}{3}* \frac{ \sqrt{3}}{2}=- \frac{ \sqrt{3} }{3}
ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Алгебра
MiKaSaKuN MiKaSaKuN  19.02.2021 12:36
Найди наименьший положительный период функции y = sin (4x+1)...
Эверяшка Эверяшка  19.02.2021 12:38
(2-3b) (2 a+3b)= ? (1-a) =?​...
innamatvijchuk innamatvijchuk  19.02.2021 12:39
я правильно сделала если не то исправьте надо было решить уравнение графическ...
мирэлюзий мирэлюзий  19.02.2021 12:40
Определи число корней квадратного уравнения 4х^2+17х+1=0 ....
оксана731 оксана731  19.02.2021 12:41
Найди корни квадратного уравнения х^2+4х+3=0 (первым вводи больший корень; если корни одинаковые, впиши одинаковые числа в оба окошка). х1 = ; х2 = ....
АБН2014 АБН2014  19.02.2021 12:41
Вычислите г) 63^2-45^2/24^2-36...
ArtemTony ArtemTony  19.02.2021 12:42
До ть будь ласка, ів♥️♥️♥️​...
weazelhubozcy1c weazelhubozcy1c  19.02.2021 12:42
Добрые люди сократите дробь.​...
кор17 кор17  19.02.2021 12:42
Найдите сумму первых пятидесяти членов арифметической прогрессии у которой с1=24 с50=98​...
НатальяДубкова НатальяДубкова  19.02.2021 12:42
пони В открывшемся зале находилась пирамида из разноцветных...

Популярные вопросы