Интеграл и его применение

1.Найти первообразную для функции f(x)=x5 +2x-4

2. Доказать, что функция F(x)=2sinx +3x является первообразной для функции f(x)=2cosx+3.

3.Найти для функции у=х такую первообразною,чтобы ее график проходил через точку Р(2;5).

4.Найти площадь фигуры ,ограниченной графиком функций у=х2 и у=4х-х2 .

5.Найти площадь фигуры ,ограниченной линиями: у=х2-4, у=х2-1, х=-2, х=2.

6.Производительность труда бригады рабочих в течение смены определяется по формуле f(t)=-2,53t2+24,75t+111,1,где t-рабочее время в часах.Определить объем продукции,изготовленной за 5 рабочих часов.

Ответы

BarcelonaReal 04.09.2020 13:20

1. ОТВЕТ: например,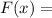 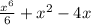F(x)= $\frac{x^6}{6}+x^2-4x$ , поскольку F'(x) = f(x) .

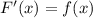Общий вид первообразных -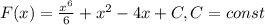 $F(x)=\frac{x^6}{6}+x^2-4x+C, C=const$

2. Докажем, что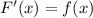 F'(x)=f(x) :

$F'(x)=(2\sin x+3x)'=2(\sin x)'+3x'=2\cos x+3=f(x)$ .

Что и требовалось доказать.

3. Общий вид первообразных функции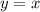 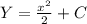y=x - $Y=\frac{x^2}{2}+C$ , где 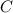- некоторое постоянное число. Если график первообразной проходит через точку 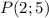P(2;5) , то это значит, что при подстановке 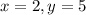x=2, y=5 получим верное равенство:

$5=\frac{2^2}{2}+C;\\\\5=2+C\Rightarrow C=3.$

Искомая первообразная -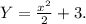 $Y=\frac{x^2}{2}+3.$

ОТВЕТ: Y = x²/2 + 3.

4. Графики функции - во вложении 1. Площадь заданной фигуры заштрихована красным.

Поскольку график функции y = 4x - x² на отрезке [0; 2] располагается как минимум не ниже графика функции y = x² (выполняется неравенство 4x - x² ≥ x²), то площадь будет иметь вид

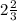$S=\int\limits^2_0 {(4x-x^2-x^2)} \, dx =\int\limits^2_0 {(4x-2x^2)} \, dx =(2x^2-\frac{2x^3}{3})|^2_0=(2\cdot2^2-\frac{2\cdot2^3}{3})-(2\cdot0^2-\frac{2\cdot0^3}{3})=8-\frac{16}{3}=8-5\frac{1}{3}=2\frac{2}{3}.$

ОТВЕТ: $2\frac{2}{3}$ кв. ед.

5. Графики - во вложении 2. Площадь заданной фигуры заштрихована красным.

Поскольку на отрезке (-2; 2) график функции y = x² - 1 располагается выше графика функции y = x² - 4 (выполняется равенство x² - 1 > x² - 4), то площадь будет иметь вид

$S=|\int\limits^2_{-2} {[x^2-1-(x^2-4)]} \, dx |=\int\limits^2_{-2} {3} \, dx= (3x)|_{-2}^2=3\cdot2-[3\cdot(-2)]=6+6=12$

ОТВЕТ: 12 кв. ед.

6. Объем выполненной работы A(t) с момента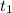 t_1 по момент 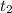t_2 согласно механическому смыслу определенного интеграла есть значение выражения интеграла

$\int\limits^{t_2}_{t_1} {f(t)} \, dt$

Имеем:

$A(t)=\int\limits^5_0 {(-2,53t^2+24,75t+111,1)} \, dt=(\frac{-2,53t^3}{3}+\frac{24,75t^2}{2}+111,1t)|_0^5=-\frac{253\cdot5^3}{300}+\frac{2475\cdot5^2}{200}+111,1\cdot5\approx760$