1. Алгебра
  2. (х2-3х+1)(х2+3х+2)(х2-9х+20)=-30

(х2-3х+1)(х2+3х+2)(х2-9х+20)=-30

volodya13031 volodya13031    3   02.08.2020 00:48    0

Ответы
дибилон1 дибилон1  15.10.2020 15:38

\dfrac{3\pm\sqrt{29}}{2},\dfrac{3\pm\sqrt{25\pm 4\sqrt{30}}}{2}

Объяснение:

Рассмотрим две последние скобки:

(x^2+3x+2)(x^2-9x+20)=(x+2)(x+1)(x-4)(x-5)=\\=(x+2)(x-5)(x+1)(x-4)=(x^2-3x-10)(x^2-3x-4)

Тогда уравнение имеет вид:

(x^2-3x+1)(x^2-3x-10)(x^2-3x-4)=-30

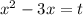Пусть x^2-3x=t:

(t+1)(t-10)(t-4)+30=0\\t^3-13t+26t+70=0

Заметим, что t = 5 — корень уравнения. Тогда, поделив столбиком левую часть на (t - 5), получим разложение левой части на множители:

(t-5)(t^2-8t-14)=0\\t=5;4\pm\sqrt{30}

1)\ x^2-3x-5=0\\x=\dfrac{3\pm\sqrt{29}}{2}\\2)\ x^2-3x-4+\sqrt{30}=0\\D=25-4\sqrt{30}0\\x=\dfrac{3\pm\sqrt{25-4\sqrt{30}}}{2}\\3)\ x^2-3x-4-\sqrt{30}=0\\x=\dfrac{3\pm\sqrt{25+4\sqrt{30}}}{2}

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Алгебра
olesyamolyanova olesyamolyanova  13.09.2019 22:20
Числитель на 5 меньше знаменателя.если к числителю прибавить 14, а из знаменателя вычесть 1,то получим дробь обратную дробь.найдите исходную дробь....
jkazlova jkazlova  13.09.2019 22:20
Игральные кости бросают дважды. найдите вероятность того что хотя бы 1 раз выпадет 6 очков？...
elenakovaleskau elenakovaleskau  12.09.2019 22:10
График какой функции получится, если параболу y=2,7x^2 перенести на 38 ед. масштаба влево и на 98 ед. масштаба вниз?...
misha426 misha426  12.09.2019 22:10
11/6 p^4 q^2+5/12p^4q^2-2 5/9p^4d^2 !...
farangizuk farangizuk  12.09.2019 22:10
Дано: треугольник авс угол а равен 60° сторона с равна 10 сторона в равна 7 найти: сторону а...
nikita2455 nikita2455  12.09.2019 22:10
Всумме возраст толи и его папы и дедушки составлять 121 будет известно что папа три раза старше толи на 23 года младше дедушке на сколько лет дедушка старше толи?...
UnicornAshad UnicornAshad  25.08.2019 19:00
Преобразуйте квадрат двучлена в многочлен стандратного вида, если можно, с объяснениями а) (a³+3b)² б)(4x² - 3c)² в)(5m²+3n²)² г) (6p² - 8g³)²...
msembinov msembinov  25.08.2019 19:00
Выражение (с-2)(с+-1)^2= 3 (а+с)^2-6ac=...
dashagokova20000000 dashagokova20000000  25.08.2019 19:00
1) клиент положил в банк 30000 рублей с ежеквартальным начислением 3% сроком на полтора года. какая сумма по будет им получена в конце года?...
РУСЛАН113228 РУСЛАН113228  25.08.2019 19:00
Вычислите (-3-4i/-3+4i)+(-3+4i/-3-4i)...

Популярные вопросы