(х^7)^3*(х^3)^9:(х^4)^6/х^23=4112
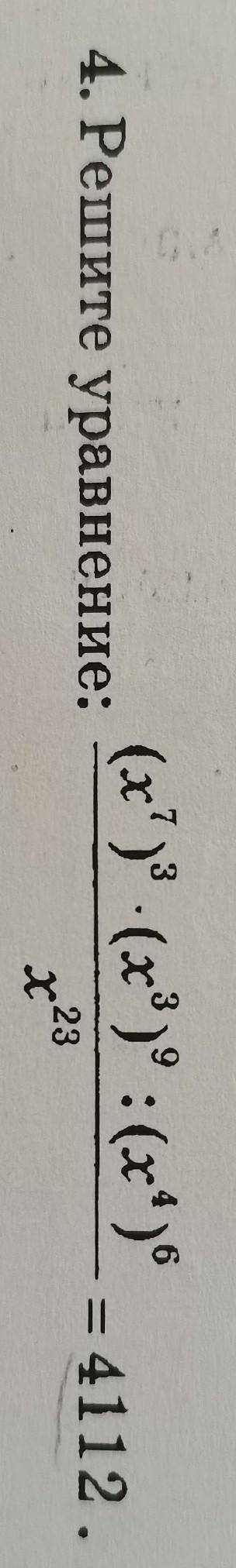
Другие вопросы по теме Алгебра
Популярные вопросы
- Решите -2:4/15-(55 29/35+32 7/20-12 5/28- 73 31/88 8/9-17 1/2:1/5+32/45+9/10+10*(50...
2 - Условие задания: 2 Б.Распредели словосочетания на две группы...
3 - У якому документи знайшла відображення подія про яку йдеться...
2 - Сочинение на тему человек на войне по рассказу Судьба человека...
1 - Давні гори між давньою і молодою платформам--...
2 - Археологиялык ескерткіштерді атап, ерекшелігін сипаттаныз. Сак,...
3 - Итоговый тест по музыке в 6 классе 1. Музыка – это: А) искусство,...
1 - 2. Как меняется настроение в стихотворении «Русалка» Лермонтова?...
2 - Задание 2 Прочитайте тексты, выполните задания.1. Сравните два...
2 - 5. Властивість, яка є загальною для нерозчинних основ та солей-це...
3
То есть, (х^7)^3 = х^(7*3) = х^21.
Точно также, выражение (х^3)^9 означает возвести х в 3-ю степень, а потом результат возведения в 9-ю степень.
То есть, (х^3)^9 = х^(3*9) = х^27.
Теперь, объединяем все выражение в скобках: (х^7)^3 * (х^3)^9 = х^21 * х^27.
Чтобы умножить два выражения с одинаковой базой, нужно сложить их показатели степеней.
Таким образом, х^21 * х^27 = x^(21+27) = x^48.
Теперь, перейдем к делению. У нас есть выражение (х^4)^6.
Возвести х в 4-ю степень и результат возведения в 6-ю степень:
(х^4)^6 = х^(4*6) = х^24.
Теперь, разделим выражение х^48 на х^24:
х^48 / х^24 = х^(48-24) = х^24.
Осталось только разделить полученное выражение х^24 на х^23.
х^24 / х^23 = х^(24-23) = х^1 = x.
Так как нам дано, что результат этой дроби равен 4112, мы можем записать уравнение:
x = 4112.
Таким образом, ответ на данный вопрос: x = 4112.