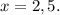(х-5)² -х ²=0
Решите от а до я откуда 10х и 25х появляются, благодарю...
Другие вопросы по теме Алгебра
Популярные вопросы
- Назовите главную тему рассказа в.в.набокова рождество . а) тема отцов...
2 - Какую работу совершит двигатель мощностью 100квт за 20 минут?...
3 - Музыка выписать произведения где есть тема любви (музыка) например:...
2 - 1.что такое средство массовой коммуникации? 2.какие средства коммуникации...
2 - Определите среднюю мощность насоса , который подаёт 45 кг воды на...
3 - Сосмавит 5 предложений на тему holiday...
3 - Записать уравнения реакций в молекулярном и иоанном виде между веществами...
3 - There are different ways of travelling. what way of travelling do...
3 - Пять целых три пятых икс минус две целых три десятых равно ноль целых...
3 - Угол при вершине равнобедренного треугольника равен 80 градусов найдите...
3
Здесь можно пойти двумя путями.
1) Через формулу квадрата разности (раскрыть первые скобки и решить уравнение). Выглядит она следующим образом: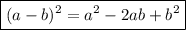
2) Через формулу разности квадратов (т.к. мы замечаем, что и уменьшаемое, и вычитаемое имеют четную степень). Выглядит она следующим образом: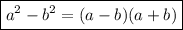 .
.
Первый вариант решения.
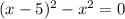
Замечаем, что уменьшаемое представляет собой квадрат разности. По формуле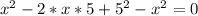
Далееответ: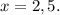
Второй вариант решения.
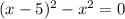
Замечаем, что уменьшаемое и вычитаемое образуют собой разность квадратов. Применяем формулуответ: