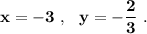(х-3у+1)^2+(х+3)^2=0
решить уравнение!
Алгебра, 7 класс.
Другие вопросы по теме Алгебра
Популярные вопросы
- Выпиши из текста по 1 существительному в 1, 2 и 3 склонениях. 1 склонение2...
3 - люди.4. Выпишите из текста 2 словосочетания, которые использует автор для...
1 - Прослушать все 3 части сонаты Бетховена и дать краткую хар-ку каждой части...
2 - Задача 2. Поженились мужчина брюнет (С) правша(Д) и блондинка (c) левша (д)....
2 - Написать полные и сокращенные уравнения реакции- 2 HCl + Mg → H2 + MgCl2...
1 - помагите Мне сегодня нужна прям сейчас. Обесните причины свертывания НЭП?...
2 - Спільне між онєгіном і пушкіном...
2 - Какую из моделей социально-экономического развития можно было бы внедрить...
1 - Раскройте скобки и приведите подобные слагаемые в выражении: 8( х – 0,4 )...
1 - Підкресліть граматичну основу та визначте вид односкладного речення. РеченняУсяке...
3
Решение.
Квадрат любого выражения может принимать только неотрицательные значения , то есть либо положительные значения, либо 0 .
Поэтому сумма двух неотрицательных выражений тоже может быть только неотрицательной . А чтобы эта сумма дала в результате 0, надо, чтобы оба неотрицательных выражения принимали одновременно значения, равные 0 .
Поэтому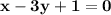 и
и  одновременно (можно было записать системой).
одновременно (можно было записать системой).
Из второго равенства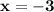 . Подставим это в первое равенство.
. Подставим это в первое равенство.
ответ: