: ( х-1 )|х²+1| + |х-1| (х²+1) = 0

Другие вопросы по теме Алгебра
Популярные вопросы
- Чем отличается современная война от ?...
2 - Почему конденсатор с двухслойным диэлетриком эквивалентен двум посдедовательно...
2 - 1. В трапеції сума кутів при одній з основ дорівнює 90⁰. Довести, що сума...
2 - Протягом тижня три кур єри дроставили 638 пакетів. кількість пакетів,...
1 - Нужно расставить химические символы и их значение...
1 - До іть! 8 клас! Одне запитання......
3 - Порівняльна характеристика двох високорозвинених країн Європи План виконання...
1 - с 7 заданием ключом дам 50 б...
3 - Характеристика главных героев барышни крестьянки с цитатами...
2 - Подскажите что вставлять в эту формулу или хотябы её правильное название...
1
Объяснение:
х²+1 всегда больше нуля, значит просто опускаем модуль
Объединяем:
ответ: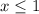
ответ: хЄ (- ∞ ; 1 ] .
Объяснение:
( x - 1 )| x² + 1 | + | x - 1 |( x² + 1 ) = 0 ;
( x - 1 )( x² + 1 ) + | x - 1 |( x² + 1 ) = 0 ;
( x² + 1 )( x - 1 + | x - 1 | ) = 0 ;
x² + 1 ≠ 0 або x - 1 + | x - 1 | = 0 ;
розв"язуємо останнє рівняння :
| x - 1 | = - х + 1 ;
вираз під модулем дорівнює 0 при х = 1 .
1) х ≤ 1 , тоді - ( x - 1 ) = - ( x - 1 ) ; правильна рівність при хЄ (- ∞ ; 1 ] ;
2) x > 1 , тоді x - 1 = - х + 1 ; > 2x = 2 ; > x = 1 ∉ ( 1 ; + ∞ ) .
В - дь : хЄ (- ∞ ; 1 ] .