Группа студентов, состоящая из 30 человек получила на экзамене оценки 2, 3 , 4 , 5 . сумма полученных оценок равна 93, причем троек было больше,

Question

Алгебра: Группа студентов, состоящая из 30 человек получила на экзамене оценки 2, 3 , 4 , 5 . сумма полученных оценок равна 93, причем троек было больше, чем пятерок, и меньше, чем четверок. кроме того, число четверок делилось на 10, а число пятерок было четным. сколько каких оценок получили студенты группы?

jokjok1337 · Answer

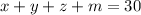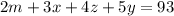Пусть число: x - троек, у - пятерок, z - четверок, m - двоек. Всего сдавали экзамен 30 студентов. x+y+z+m=30 , всего полученных оценок - 93, для него уравнение 2m+3x+4z+5y=93 .

Составим систему по условию:

$\begin{cases}&\text{}x+y+z+m=30\\&\text{}2m+3x+4z+5y=93\\&\text{}xy\\&\text{}x$

Решением этой системы подходят такие натуральные значения n = k = 1 и получим z = 10 и y = 2, подставляя в систему получим

$\begin{cases}&\text{}x+2+10+m=30\\&\text{}2m+3x+4\cdot 10+5\cdot 2=93\end{cases}~~~\Rightarrow~~\begin{cases}&\text{}x+m=18\\&\text{}2m+3x=43\end{cases}\\ \\ \\ \Rightarrow~~~\begin{cases}&\text{}x=18-m\\&\text{}2m+3\cdot(18-m)=43\end{cases}\\ \\ \\ 2m+54-3m=43\\ \\ m=11\\ \\ x=7$

Таким образом, 11 двоек, 7 троек, 10 четверок и 2 пятерок.

P.S. для остальных натуральных значений k,n нет других решений.

Популярные вопросы