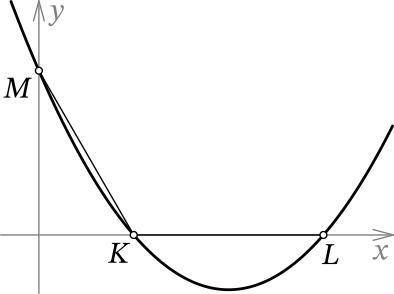
График квадратного трёхчлена y = 2/√3 * x^2 + bx + c пересекает оси координат в трёх точках K, L и M, как на рисунке ниже. Оказалось, что KL=KM и ∠LKM=120∘. Найдите корни данного трёхчлена. Введите оба корня — каждое число в отдельное поле ввода в произвольном порядке.

Дан график  y = (2/√3)x² + bx + c и  условия: KL=KM, ∠LKM=120∘, где L, K и M точки пересечения осей.

Примем координаты корней на оси Ох: х1 и х2.

Координата точки М по у равна коэффициенту с из уравнения.

Из треугольника МОК с учётом угла 180 - 120 = 60 находим соотношение: с = х1*tg60 = x1*√3.

Далее используем равенство KL=KM.

KL=KM = √((х1)² + (x1*√3)²) = √((х1)² + 3(х1)²)  = √(4((х1)²) = 2*х1.

Отсюда находим: х2 = х1 + 2х1 = 3х1.

Далее используем теорему Виета для корней.

Для этого надо разделить коэффициенты уравнения на а (2/√3).

Получаем уравнение y = x² +(b/(2/√3))x + c/(2/√3).

Для определения корней правую часть приравняем нулю.

x² +(b/(2/√3))x + c/(2/√3) = 0.

По Виета х1*х2 = c/(2/√3). Заменим с = x1*√3  и х2 = 3х1.

3(х1)² = x1*√3/(2/√3). После сокращения получаем:

х1 = 1/2. Это найден первый корень.

Второй равен 3х1 = 3*(1/2) = 3/2.

ответ: корни равны (1/2) и (3/2).