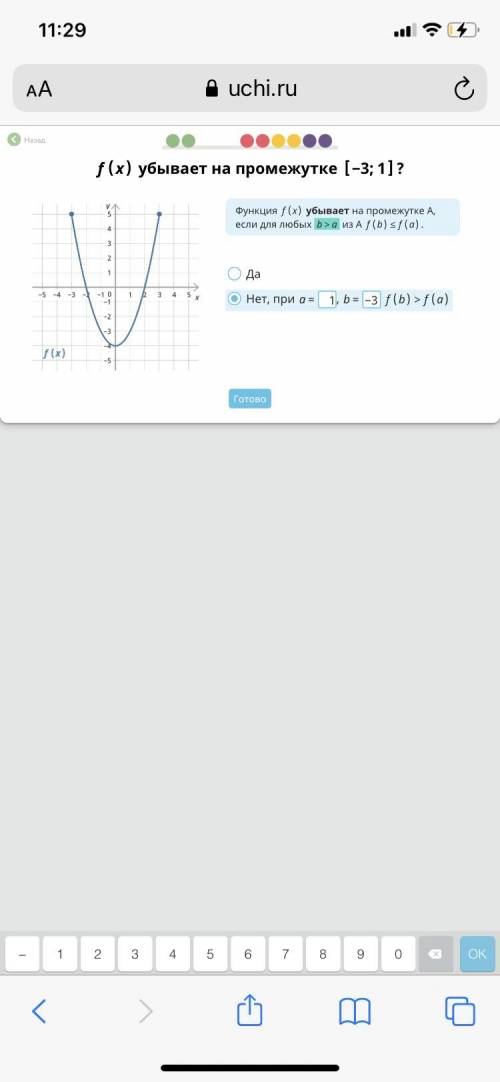
Функция f(x) убывает на промежутке -3;1 ?
При каких а и б она не убывает

Для того чтобы понять при каких значениях a и b функция не будет убывать на промежутке -3;1, необходимо проанализировать график функции f(x).

На графике видно, что функция убывает на промежутке -3 до некоторого значения x1 и после него функция начинает возрастать до значения x2, а затем продолжает убывать. Задача состоит в том, чтобы найти значения a и b, при которых функция начинает возрастать вместо убывания или не убывает вообще.

Подходящей областью для исследования является промежуток между x1 и x2. Рассмотрим каждый отрезок отдельно.

Отрезок A: -3 < x < x1
На этом отрезке функция убывает. Это значит, что при любых значениях a и b функция будет убывать на этом отрезке.

Отрезок B: x1 < x < x2
На этом отрезке функция может либо убывать, либо возрастать. Это означает, что есть такие значения a и b, при которых функция возрастает на этом отрезке или не убывает вообще. Чтобы определить, при каких значениях a и b это происходит, необходимо проанализировать уравнение функции.

Уравнение функции имеет вид:
f(x) = ax^2 + 3x + b

Чтобы определить какие значения a и b не убывает на отрезке B, необходимо найти производную функции f'(x) и проанализировать её знаки на отрезке B.

f'(x) = 2ax + 3

Знак производной f'(x) определяет убывание или возрастание функции f(x). При положительном знаке производной функция возрастает, а при отрицательном знаке функция убывает.

Теперь найдем значение x1 и x2, координаты точек перегиба функции. Для этого приравняем производную к нулю и решим полученное уравнение:

2ax + 3 = 0
2ax = -3
x = -3/(2a)

Мы получили значение x1, которое является координатой точки перегиба.

Теперь найдем производную второго порядка (f''(x)) функции f(x) и также проанализируем её знаки.

f''(x) = 2a

Знак второй производной f''(x) определяет выпуклость или вогнутость графика функции. При положительном значении f''(x) график функции будет вогнут вверх, а при отрицательном значении график функции будет выпуклый вниз.

Теперь мы можем проанализировать, при каких значениях a и b функция не убывает на отрезке B.

1. Если a > 0, то функция будет возрастать на отрезке B. Это происходит из-за положительного знака первой производной f'(x) и отрицательного значения коэффициента a.

2. Если a < 0, то необходимо рассмотреть случаи:
а) Если a < 0 и f''(x) > 0, то функция будет возрастать на отрезке B из-за отрицательного значения функции f''(x) и a.
б) Если a < 0 и f''(x) < 0, то функция будет убывать на отрезке B из-за положительного значения функции f''(x) и a.
в) Если a < 0 и f''(x) = 0, то функция может являться периодической, и ее поведение на отрезке B будет зависеть от значения коэффициента b.

Таким образом, при a > 0 или при a < 0 и f''(x) > 0 функция не будет убывать на отрезке B, независимо от значения коэффициента b.

Анализируя график функции f(x), можно заметить, что функция не убывает на этом отрезке, если a > 0 или a < 0 и b > 1.

Таким образом, функция не будет убывать на промежутке -3;1 при a > 0 или при a < 0 и b > 1.