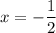Функцію задано формулою f(x)=x-4/3x^3
Знайти критичні точки функції f(x) та найбільше й найменше значення функції на відрізку [0;1]
Другие вопросы по теме Алгебра
Популярные вопросы
- Обмен товара на деньги и денег на товар «ляговтор»...
3 - 7. закрытые двери легко отворялись, потому что … а) чернушка кудахтала...
3 - X-2/3 + 1/3 линейные уравнения нужен полный ответ...
3 - Нарисуй, как ты представляешь себе этих персонажей : домовой, водяной,...
3 - Y=2^cosx² найти производную y с объяснением...
1 - Напишите конспект по теме добываение огня , разведение костра и 2 устройство...
2 - Сложносочиненные предложения с соединительными союзами...
2 - Чи лежить сніг на вершині г.кіліманджара(5895м) в продовж року, якщо...
2 - Если бы ученики захотели выяснить, влияет ли наличие почвы в стакане...
2 - По условию y = 3 - x, связывающему координаты точек, составьте таблицу...
2
Відповідь:
Пояснення:
Для нахождения критических точек ищем корни уравнения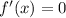
То есть если знаки расставлять, то получим -+-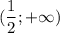
То есть на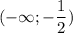 функция убывает, на
функция убывает, на 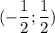 возрастает, на
возрастает, на 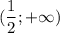 убывает.
убывает.
Посчитаем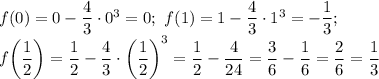
То есть на отрезке [0;1]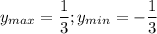 , точка экстремума
, точка экстремума 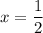
Не на отрезке [0;1] есть ещё точка экстремума