Функція задана формулою 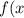=x^{2} -3x-4) 1) побудуйте графік функції та вкажіть нулі функції, якщо вони існують 2) знайдіть значення
1) побудуйте графік функції та вкажіть нулі функції, якщо вони існують 2) знайдіть значення  , за якого похідна функції дорівнює 1 3) запишіть рівняння дотичної до графіка функції в точці
, за якого похідна функції дорівнює 1 3) запишіть рівняння дотичної до графіка функції в точці 
Другие вопросы по теме Алгебра
Популярные вопросы
- Для угла 4 односторонним будет угол а) 1 б) 8 в) 5 г) 3...
1 - Краткий анализ к лесной царь в.а. жуковский...
2 - Постройте график функции (15б)...
2 - До завтра надо сделать а я не знаю как это делать выручайте ...
3 - 30 ! ! изображение барыни в повести ...
1 - Что общего у фонтана-героя первой строфы и ,,водомёта смертной...
3 - Попс формуласы 4 сөйлемен баиыр баян...
1 - №6 зертханалық жұмыс 8 сынып тақырбы өткізгіштерді паралель жалғауды...
3 - Просклонять lucy and ann draw a beautiful portrait during the...
3 - Составьте 4 предложения где 1. красивее это прилагательное 2....
3
f(x)=x²-3x-4 парабола, ветви вверх, вершина в точке (1,5 ; -6,25) .
1) нули функции находим по теореме Виета из уравнения х²-3х-4=0 :
х₁=-1 , х₂=4 ;
2) f'(x)=2x-3 , 2x-3=1 , 2x=4 , x₀=2 ;
3) уравнение касательной к параболе в точке х₀=2:
f'(x₀)=f'(2)=1 , f(2)=4-6-4= -6 ,
y=f(x₀)+f'(x₀)·(x-x₀) ⇒ y= -6+1·(x-2) , y=x-8 .
1)f(x)=0
x²-3x-4=0
D=9+16=25=5²
x=(3±5)/2
x1=4;x2=-1
2)x0=3/2
3)f(x0)=(3/2)²-3*3/2-4=9/4-(9/2)-4=
(9-18-16)/4=-25/4