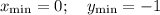F(x)=(x²-1)/(x²+1) найти промежутки возрастания и убывания функции и точки экстремума.
Другие вопросы по теме Алгебра
Популярные вопросы
- Aob бұрышының градустық өлшемі жазыңқы бұрыштың 65%-іне тең. aob...
3 - Спільні та відмінні ознаки і родинно побутових пісень?...
2 - Подберите родовое слово,объединяющее в одну тематическую группу...
1 - Во сколько раз звезда 2-ой величины ярче звезды 4-ой величины,если...
3 - Вверх по наклонной плоскости с углом а=45 градусов к горизонту...
1 - Площадь первого участка земли 375 м 2 площадь второго в 3 раза...
2 - Составь с существительными 2 1.игрушка, очередь, фотография, поэзия,...
2 - )расставьте скобки,чтобы равенство стало верный: 0,5+0,5: 0,5+0,5:...
1 - Переказ на тему правда про прометея ) строчно ето на завтра 15...
2 - Составьте по два словосочетания. и по одному предложению со словами...
3
Определим производную функции по формуле: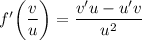
Определим критические точки, приравняв к нулю значение производной:
Определим промежутки возрастания, убывания и точки экстремума (выбираем из каждого промежутка какое-нибудь число и подставляем его в производную, и проверяем её знак):
Итак,
1) функция возрастает на промежутке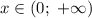
2) функция убывает на промежутке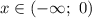
3)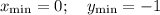
Для нахождения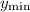 мы подставляем значение
мы подставляем значение  в значение функции.
в значение функции.
1) функция возрастает на промежутке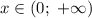
2) функция убывает на промежутке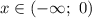
3)