F(x)=tg2x/1+cosx
Определить четность или нечётность функции
!
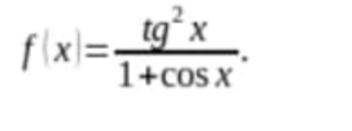
Другие вопросы по теме Алгебра
Популярные вопросы
- 1)f(x) = корень из x, x0=42)f(x)=x³, x0= -1...
2 - с С.Р. по геометрии1) Хорды АВ и СД пересекаются в точке Е. АЕ=3см,СЕ=2см,ВЕ=4см,...
3 - заменить родину местоимением родина начинается с твоего порога...
1 - Скласти 4 , щоб прикладка з сполучником як відокремлювалося...
3 - Написать 15 предложений на тему My favourite holiday (на английском)...
1 - Несколько во с ответами по теме англия экономическое лидерство и политические...
1 - Каковы были причины поражения восставших? CРОЧНО...
2 - Брусок, имеющий форму прямоугольного параллелепипеда, поместили в жидкость...
1 - Почему рассказ Пришвина называется Москва-река...
1 - FeCl2: Ag, Pb(NO3)2, Al(OH)3, KOH, Na, Li2O, H2SO3, SiO2...
2
1. Четность функции: F(x) является четной функцией, если выполняется условие F(-x) = F(x) для любого значения x в области определения функции.
2. Нечетность функции: F(x) является нечетной функцией, если выполняется условие F(-x) = -F(x) для любого значения x в области определения функции.
В данном случае, функция F(x) = tg^2x/(1+cosx). Давайте проверим ее на четность и нечетность по очереди.
1. Проверка на четность: Заменяем x на -x в исходной функции и сравниваем с исходной функцией.
F(-x) = tg^2(-x)/(1+cos(-x))
Так как тангенс является нечетной функцией, то его квадрат также будет нечетным, а косинус является четной функцией, то cos(-x) = cos(x), а (1+cos(-x)) = (1+cos(x)). Тогда:
F(-x) = [tg(-x)]^2/(1+cos(-x))
F(-x) = [(-tgx)]^2/(1+cos(x))
F(-x) = tg^2x/(1+cos(x)) = F(x)
Таким образом, функция F(x) является четной функцией.
2. Проверка на нечетность: Заменяем x на -x в исходной функции и сравниваем с исходной функцией, умноженной на -1.
-F(x) = -(tg^2x/(1+cosx))
-F(x) = -tg^2x/(1+cosx)
Таким образом, функция -F(x) не равна F(-x), а на самом деле противоположна ей.
Итак, функция F(x) является только четной функцией.