Есть простое выражение, где надобно доказать, что результат целое число... 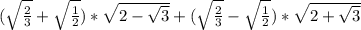
И что-то я никак не вижу решения для этого выражения... Кто-нибудь видит что здесь надо применить?
Другие вопросы по теме Алгебра
Популярные вопросы
- Современные потребители редко серьёзно воспринимают рекламу, понимая,...
1 - Напишите кратко о современном петербурге...
3 - Научная скпзка по биологии про инфузорию туфельку...
3 - Хлодвиг и христианская церковь кратко...
3 - Разобрать слова под цыфрой 1 вредный...
3 - Выполни сложение столбиком 361×27= 901×204= 5671 ×340=...
3 - Кумирами молодежи герои произведений: рахметов н.г. чернышеского и базаров...
2 - Реши уравнения: (а + 9) - 209. 2) х ÷ 7 = 8 3) b × 5 = 45...
2 - По какому правилу составлен ряд чисел..1.2.4.8....
2 - Уджека было 16 кур ,а гусей на 4 больше скколько гусей у джека сколько...
3
При решении были применены формулы сложного радикала :