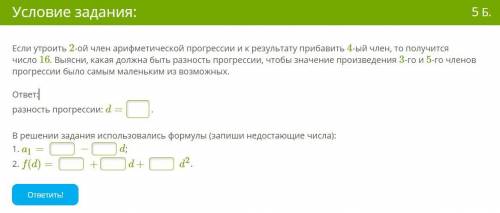
Если утроить 2-ой член арифметической прогрессии и к результату прибавить 4-ый член, то получится число 16. Выясни, какая должна быть разность прогрессии, чтобы значение произведения 3-го и 5-го членов прогрессии было самым маленьким из возможных.

Добрый день! Давайте рассмотрим задачу по порядку.

У нас есть арифметическая прогрессия, где каждый следующий член получается путем добавления одного и того же значения к предыдущему члену. Пусть разность этой прогрессии равна d. Тогда второй член можно представить в виде a + d, где a - первый член прогрессии.

Согласно условию, если утроить второй член и прибавить к нему четвертый член, мы получим число 16. Из этого следует уравнение:

3(a + d) + (a + 3d) = 16.

Раскрываем скобки и собираем подобные слагаемые:

4a + 6d = 16.

Полученное уравнение (1) будет нам полезно в дальнейшем.

Теперь давайте перейдем к второй части вопроса. Мы хотим найти разность прогрессии (d), при которой значение произведения третьего (a + 2d) и пятого (a + 4d) членов будет самым маленьким.

Запишем произведение третьего и пятого членов прогрессии:

(a + 2d)(a + 4d).

Раскрываем скобки и собираем одинаковые слагаемые:

a^2 + 6ad + 8d^2.

Нам нужно минимизировать это выражение. Для этого мы можем воспользоваться двумя способами: аналитическим и графическим.

При помощи аналитического метода мы можем найти минимум данной функции. Для этого рассмотрим выражение a^2 + 6ad + 8d^2 как квадратное трехчленное уравнение относительно переменной a:

a^2 + 6ad + 8d^2 = a^2 + 2ad + 4d^2 + 4ad + 4d^2 = (a + 2d)^2 + 4ad + 4d^2.

Выражение в скобках (a + 2d)^2 является положительным и не может быть отрицательным, поэтому минимум произведения будет достигаться, когда 4ad + 4d^2 = 0. Учитывая, что a и d не могут быть нулевыми (иначе прогрессия будет нулевой), мы можем делить данное уравнение на 4d и получить:

a + d = 0.

Отсюда следует, что значение d может быть выбрано произвольно, и разность прогрессии будет равна -a.

Теперь давайте вернемся к уравнению (1), которое мы получили ранее:

4a + 6d = 16.

Мы знаем, что a + d = 0, поэтому мы можем заменить a в этом уравнении на -d:

4(-d) + 6d = 16.

Упрощаем:

-4d + 6d = 16,
2d = 16,
d = 8.

Таким образом, разность прогрессии должна быть равна 8, чтобы значение произведения третьего и пятого членов было самым маленьким из возможных.

Надеюсь, это разъясняет задачу. Если возникнут дополнительные вопросы, пожалуйста, не стесняйтесь задавать их!