Если tgх=4/3, а tgy=1/4, найдите tg(х+y)
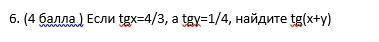
Другие вопросы по теме Алгебра
Популярные вопросы
- 10 ! вычислить с решением по действиям...
3 - Двузначное число в 7 раз больше суммы своих цифр и на 52 больше произведения...
2 - Как прочитать словами стих без перевода 30 days has september,april,june...
3 - Раствор калий гидроксид m = 200 г , w = 15 %взаимодействует с ортофосфарной...
3 - 6. техникалық құралдар мен ғаламтор ұстазды алмастыра ала ма? өз ойларыңды...
2 - Y=(x+1)*(x+2)*(x+4)/(x+4) определитель при каких значениях m прямая...
2 - Какую оценку получит мальчик прыгнувший 216 местров...
2 - Как вы думаете, какими качествами обладал и. п. ку-либин? почему энтузиаста-изобретателя...
3 - С,буду вам искренне 98 желательно что-бы ответ был с фотографией,заранее...
1 - Запишите многочлен в стандартном виде...
3
Объяснение:
tg x*tg y = 1/3
{ sin x*sin y = 1/4
Преобразуем так
{ sin x/cos x*sin y/cos y = (sin x*sin y)/(cos x*cos y) = 1/3
{ sin x*sin y = 1/4
Отсюда
{ sin x*sin y = 1/4
{ cos x*cos y = ( sin x*sin y ) / (1/3) = (1/4) / (1/3) = 3/4
При этом мы знаем, что sin^2 y + cos^2 y = 1; cos y = √(1 - sin^2 y)
sin y = 1/(4sin x); cos y = √(1 - 1/(16sin^2 x)) = √(16sin^2 x - 1) / (4sin x)
Подставляем во 2 уравнение
cos x* √(16sin^2 x - 1) / (4sin x) = 3/4
Умножаем все на 4
tg x* √(16sin^2 x - 1) = 3
√(16sin^2 x - 1) = 3/tg x = 3ctg x
16sin^2 x = 1 + 9ctg^2 x
Есть формула
sin^2 a = 1/(1 + ctg^2 a)
Подставляем
16 / (1 + ctg^2 x) = 1 + 9ctg^2 x
16 = (1 + 9ctg^2 x)(1 + ctg^2 x)
Замена ctg^2 x = t >= 0 при любом х
16 = (1 + 9t)(1 + t) = 1 + 10t + 9t^2
9t^2 + 10t - 15 = 0
D/4 = 5^2 - 9(-15) = 25 + 135 = 160 = (4√10)^2
t1 = (-5 - 4√10)/9 < 0
t2 = (-5 + 4√10)/9 = ctg^2 x
1 + ctg^2 x = 1 + (4√10 - 5)/9 = (9 + 4√10 - 5)/9 = (4√10 + 4)/9
sin^2 x = 1/(1+ctg^2 x) = 9/(4(√10+1)) = 9(√10-1)/(4(10-1)) = (√10-1)/4
sin x = √(√10 - 1) / 2
x = (-1)^n*arcsin [ √(√10 - 1) / 2 ] + pi*n
sin y = 1/(4sin x) = 2/(4√(√10 - 1)) = 1/(2√(√10 - 1)) = √(√10 - 1)/(2(√10 - 1))
y = (-1)^n*arcsin [ √(√10 - 1)/(2(√10 - 1)) ] + pi*n
решение смотри на фотографии