1. Алгебра
  2. Если открыть одновременно

Если открыть одновременно две трубы, то бассейн будет наполнен за 12 ч. Если сначала наполнять бассейн только через первую трубу в течение 5 ч, а затем только через вторую течение 9 часов, то водой будет наполнен половину бассейна. За сколько часов может наполнить бассейн каждая труба, работая самостоятельно?

лучшая40 лучшая40    2   17.02.2021 22:18    4

Ответы
rrxxmarta rrxxmarta  19.03.2021 22:25

ответ: 16 и 48 часов соответственно

Объяснение:

1 - емкость бассейна;

x - скорость наполнения первой трубы;

y - скорость наполнения второй трубы;

\left \{ {{12(x+y)=1} \atop {5x+9y=\frac{1}{2} }} \right. =\left \{ {{12x+12y=1} \atop {10x+18y=1 }} \right. =\left \{ {{12\frac{1-18y}{10}+12y=1} \atop {x=\frac{1-18y}{10} }} \right.\\\\\left \{ {{\frac{12-216y}{10}+\frac{120y}{10}=1} \atop {x=\frac{1-18y}{10} }} \right.=\left \{ {{\frac{12-96y}{10}=1} \atop {x=\frac{1-18y}{10} }} \right.=\left \{ {{{12-96y}=10} \atop {x=\frac{1-18y}{10} }} \right.=\left \{ {{{-96y}=-2} \atop {x=\frac{1-18y}{10} }} \right.\\

\left \{ {{{y}=\frac{1}{48} } \atop {x=\frac{1-18\frac{1}{48}}{10}}} \right.=\left \{ {{{y}=\frac{1}{48} } \atop {x=\frac{\frac{48-18}{48}}{10}}} \right.=\left \{ {{{y}=\frac{1}{48} } \atop {x={\frac{3}{48}}}=\frac{1}{16} } \right.

наполнение первой трубой: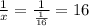 \frac{1}{x}=\frac{1}{\frac{1}{16}} =16 часов;

наполнение второй трубой: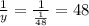 \frac{1}{y} =\frac{1}{\frac{1}{48}} =48 часов.

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Алгебра
89051330939 89051330939  29.09.2019 20:16
Туманность андромеды удалена от нас на [tex]2.3 \times 10 {}^{6} [/tex]световых лет. сколько километров до нее? ​...
anastasiabojko5 anastasiabojko5  29.09.2019 20:17
Много на фото,мне нужно решить 4 ! в начале нужно все расписать: пусть x будет и т.д...
polinasenchenk polinasenchenk  29.09.2019 21:20
При каких значения переменной дробь не имеет смысла? __x+ x(x-3)...
canimzoo canimzoo  29.09.2019 20:19
V[tex] a)\sqrt{x} = \sqrt{ - x} \\ b) x \times \sqrt{ \frac{3}{x} } + 9 = 0 \\ c)x \times \sqrt{ \frac{5}{x} } = \sqrt{ {x}^{2} } \\ d) - x \times \sqrt{ \frac{ - 4}{ x}...
tema30102008 tema30102008  29.09.2019 20:20
Обьясните как построить график функции y=|||x-3|-2|-1|​...
KaterinaKlimenko2017 KaterinaKlimenko2017  15.11.2020 16:52
Избавиться от иррациональности в знаменателе дроби (номер 5) И кому не сложно... Решите номера 7, 8 и желательно 9​...
nick121201 nick121201  15.11.2020 16:53
турист за перший день пройшов 15% усього шляху , за другий день , - 2/7 усього шляху . Який шлях пройшов турист у другий день , якщо за перший він пройшов 21 км ?​...
Brosherin Brosherin  15.11.2020 16:55
Кто мне решить эту проблему?...
сергейважный1 сергейважный1  14.05.2020 18:20
Розв яжіть рівняння 8+√x2=48−x2=4. Скільки коренів має рівняння? Якщо коренів немає, у відповідь запишіть 0.​...
Alia178 Alia178  14.05.2020 18:21
Решите желательно на листочке ​...

Популярные вопросы