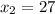если можно написать не текстом, а в тетрадке(Даю 50б)
Другие вопросы по теме Алгебра
Популярные вопросы
- Напишите характеристику унтер-офицерши из Ревизора...
3 - Куда направлена сила, что действует на электрон...
3 - Як можна назвати цю группу слів: 1. Лікург, Мойсей, Мінос, Шліман, Гомер,...
2 - Повідомлення Перікла в Афінах(7-10 речень) ...
1 - Найдите интервалы возрастания и убывания функции a) b)...
2 - 1.15. Яке з тверджень є правильним? А) якщо пряма а не паралельна прямій...
3 - В чем состояла сущность нэпа?...
2 - Металлический шар, имеющий электрический заряд q1= 6нКл привели в соприкосновение...
3 - круглий мідний стержень діаметром 10мм приварений торцем до плити з...
1 - 1 Порівняйте правління Володимира Мономаха та Мстислава Володимировича:...
3
X1=3
X2=27
Объяснение:
Одз
Применяем метод замены переменной
Получаем с виета (надеюсь знаешь как решать)
Подставляем эти корни обратно
Решаем
Получаем ответ
прощения, что не в рукописном варианте, но думаю, что ход мыслей будет понятен=)
Нужно помнить, про то, что значение x, стоящего под логарифмом - всегда строго больше нуля (ОДЗ: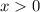 ).
).
Пусть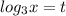 , тогда:
, тогда:
Тогда:
1).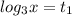
(таким числом под логарифмом будет 27: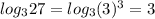 )
)
2).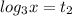
(таким числом под логарифмом будет 3: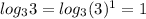 )
)
ответ: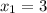 ,
,